Să se determine m∈R astfel încât sistemul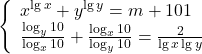 să admită soluţii reale.
să admită soluţii reale.
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Din conditiile de existenta ale logaritmilor: .
.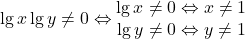
 putem folosi formula:
putem folosi formula: ![Rendered by QuickLaTeX.com \log_ab=\frac{1}{\log_ba},adevarata [tex]\forall a,b\neq 1 , a,b>0](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-92572cc0635e9444560fd4e1012764cf_l3.png)
Din conditiile de existenta ale fractiti din a doua relatie:
EDIT: Din pacate nu mi-a iesit problema si am inchis fereastra din greseala. Frumoasa solutie, domnule bedrix!
A doua ecuatie este echivalenta cu: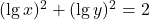 .Ce fac in continuare?
.Ce fac in continuare?
Notam x^lgx=a si y^lgy=b rezulta (lgx)^2 = lg a si (lgy)^2 = lg b , unde a>1 , b>1 (1)
Sistemul devine
a+b=m+101
lg a +lg b=2 echivalent cu a*b=100 . Recunoastem relatiile lui Viete ; formezi ecuatia de gradul 2 : z^2-S*z+P=0, determinantul >=0 adica(m+101)^2-4*100>=0 rezulta m .
Determinantul este strict mai mare ca 0,nu poate fi si egal?❓ 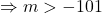
![Rendered by QuickLaTeX.com \Rightarrow m\in (-\infty ;-121]\cup [-81;+\infty )](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-215f91767e1c5c35653017534085266c_l3.png)
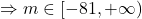 .Mai trebuie puse alte conditii?
.Mai trebuie puse alte conditii?
Din relatia 1
Din inecuatie
Am rectificat . Cred ca trebuie introdusa conditia a>1 si b>1 ca sa aiba sens lg^2.
„bedrix” a facut f. bine , pana la discriminantul ec. ale carei radcini sunt ; „a” si „b”, dar se mai pune si conditia ca „a” si „b”sa fie mai mari sau egale cu 1, pentru ca ; (lg(x))^2=lg(a) si (lg(y))^2=lg(b). Deci , fie ec. ale carei radacini sunt ; „a” si „b” ; t^2-(m+101).t+100=0 . Ca radacinile acestei ec. sa fie mai mari sau egale cu 1 trebue ca ;
-a]. discriminantul sa fie >=0,
-b[. minimul expresiei ; f(t)=t^2-(m+101).t+100 sa corespunda lui tv=(m+101)/2>1.
-c]. f(1)>=0 .
-Din b]. Rezulta ; m>-99 si din c]. m<=0. In concluzie, m apartine intervalului ; [-81 , 0] . Intrebari?
Da, de ce f(1)>=0?Daca x si y sunt diferiti de 1 nu rezulta ca si a si b sunt diferiti de 1?
Ca sa am radacini mai mari ca 1 sau egale cu 1 , trebue ca reprezentarea grafica a lui f(t), sa taie axa absciselor, la dreapta cotei 1, sau sa treaca prin 1. in cazul dat ,pentru t=1 ->f(1)>=0 si tv>1.
La a doua obs. , ai dreptate . Am uitat ca x si y sunt baze de logaritmi . Conditia c]. va fi f(1)>0 si solutia finala ; „m” apartine intervalului [-81 , 0)
Multumesc pentru ajutor🙂 .