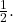Home/ Intrebari/Q 74884
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

gefest
Pe: 2011-12-07T14:57:52+02:00 In: In:

trigonometrie

Sa se arate ca daca in \triangle ABC:
a) \sin B+\cos B=\sin C+\cos C, atunci triunghiul este dreptunghic sau isoscel;
b) \cos A+\cos B-\cos(A+B)=\frac32, atunci triunghiul este echilateral.

a) Aici pot sa arat ca suma B+C este unghi drept, dar sa arat ca este triunghi isoscel nu-mi iese:
\sin B+\cos B=\sin C+\cos C\ \Leftrightarrow\ \\ \sin B-\sin C=\cos C-\cos B\ \Leftrightarrow\ \\ 2\cos\frac{B+C}{2}\sin\frac{B-C}{2}=-2\sin\frac{C+B}{2}\sin\frac{C-B}{2}\ \Leftrightarrow\ \\ 2\cos\frac{B+C}{2}\sin\frac{B-C}{2}=2\sin\frac{C+B}{2}\sin\frac{B-C}{2}\ \Leftrightarrow\ \\ \cos\frac{B+C}{2}=\sin\frac{C+B}{2}\\ \frac{B+C}{2}=\frac{\pi}{4}\ \Leftrightarrow\ B+C=\frac{\pi}{2}

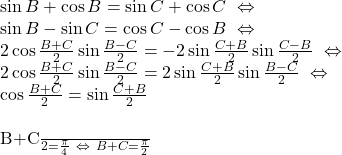
La b) n-am nicio idee. Aplicind formulele la b) complic expresia mai tare.

Similare

3 raspunsuri

  1. PhantomR
    expert (VI)

    gefest wrote: 2\cos\frac{B+C}{2}\sin\frac{B-C}{2}=2\sin\frac{C+B}{2}\sin\frac{B-C}{2}

    Aici mi se pare ca e problema. Banuind ca ati impartit cu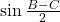 \sin\frac{B-C}{2}, acest lucru ar implica ca mai intai sa presupuneti ca este diferit de zero. 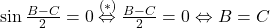\sin\frac{B-C}{2}=0 \stackrel{(*)}{\Leftrightarrow} \frac{B-C}{2}=0 \Leftrightarrow B=C, adica triunghiul ar fi isoscel intr-un caz, iar pentru a vedea daca se mai obtin si alte „solutii” presupuneti expresia diferita de zero si apoi faceti impartirea. V-as sfatui (caci cred ca si mie mi s-a intamplat sa impart cu anumite expresii care puteau lua valoare nula) sa aveti grija la impartirile de acest gen.

    NOTA: Nu sunt din pacate foarte sigur ca e corect sa folosim direct (fara mentiuni, demonstratii suplimentare) lucruri similare cu (*) (scris de mine) sau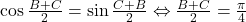 \cos\frac{B+C}{2}=\sin\frac{C+B}{2} \Leftrightarrow \frac{B+C}{2}=\frac{\pi}{4}, scris de dumneavoastra (**)

    \alpha. In rezolvarea unei ecuatii de forma: \cos\frac{B+C}{2}=\sin\frac{C+B}{2}, eu as proceda de obicei cu anumite mentiuni:
    1. B+C<180 \Rightarrow \frac{B+C}{2}<\frac{180}{2}=90
    2. B+C>0
    1.,2. \Rightarrow \cos\frac{B+C}{2}>0,\sin\frac{C+B}{2}>0 si scriind egalitatea ca \cos\frac{B+C}{2}-\sin\frac{C+B}{2}=0 si ridicand-o la patrat obtinem, folosind identitatea \sin^2x+\cos^2x=1 obtinem: 1=2\cos\frac{B+C}{2}\sin\frac{C+B}{2} sau folosind 2\sin x\cos x = sin 2x -> 1=\sin(B+C) \stackrel{0<B+C<180}{\Leftrightarrow}B+C=90 . Am lucrat in grade, sper ca nu e problema.

    \beta. In rezolvarea unei ecuatii de forma (*) \sin\frac{B-C}{2}=0 deoarece nu avem o relatie anume intre unghiuri, as presupune B\geq C \Rightarrow B-C\geq 0 \Rightarrow \frac{B-C}{2}\geq 0. Cum avem B-C<180 \Rightarrow \frac{B-C}{2}<90 (De ce? De exemplu din cauza ca B<180 iar C>0.), obtinem \frac{B-C}{2}=0 si apoi concluzia.

  2. ex-admin
    profesor

    gefest wrote: b) \cos A+\cos B-\cos(A+B)=\frac32, atunci triunghiul este echilateral.

    Eegalitatea se poate scrie echivalent

        \[ \sin \frac{A}{2}\sin \frac{B}{2}\sin \frac{C}{2} = \frac{1}{8} \]

    astfel:

        \[ \begin{array}{l} \cos A + \cos B - \cos (A + B) = \frac{3}{2} \Leftrightarrow \cos A + \cos B + \cos C = \frac{3}{2} \\ \Leftrightarrow \\ 2\cos \left( {\frac{{A + B}}{2}} \right)\cos \left( {\frac{{A - B}}{2}} \right) - 2\cos ^2 \left( {\frac{{A + B}}{2}} \right) + 1 = \frac{3}{2} \\ \Leftrightarrow \\ 2\cos \left( {\frac{{A + B}}{2}} \right) \cdot \left( {\cos \frac{{A - B}}{2} - \cos \frac{{A + B}}{2}} \right) = \frac{1}{2} \\ \Leftrightarrow \\ 2\cos \left( {\frac{{A + B}}{2}} \right) \cdot \left( {2 \cdot \sin \frac{A}{2}\sin \frac{B}{2}} \right) = \frac{1}{2} \\ \Leftrightarrow \\ \sin \frac{A}{2}\sin \frac{B}{2}\sin \frac{C}{2} = \frac{1}{8} \\ \end{array} \]

    .

    Este suficient sa demonstram ca are loc inegalitatea

        \[ \sin \frac{A}{2}\sin \frac{B}{2}\sin \frac{C}{2} \le \frac{1}{8} \]

    si ca egalitatea are loc daca si numai daca A=B=C.

    Inlocuind sinusurile prin laturi obtinem

        \[ \begin{array}{l} 8\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right) \le abc \\ \Leftrightarrow \\ \left( { - a + b + c} \right)\left( {a - b + c} \right)\left( {a + b - c} \right) \le abc. \\ \end{array} \]

    .

    Facand substitutiile

        \[ a = y + z,\,\,b = z + x,\,\,\,c = x + y \]

    se ajunge la

        \[ 8xyz \le \left( {y + z} \right)\left( {z + x} \right)\left( {x + y} \right) \]

    ,

    inegalitate care se demonstreaza prin inmultirea inegalitatii mediilor

        \[ 2\sqrt {xy} \le x + y \]

    cu celelalte doua similare.

    Evident in inegalitatea

        \[ 8xyz \le \left( {y + z} \right)\left( {z + x} \right)\left( {x + y} \right) \]

    egalitatea are loc daca si numai daca x=y=z ceea ce este echivalent cu a=b=c adica triunghiul ABC este echilateral.

  4. gefest

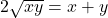    La punctul b) la inegalitatea mediei daca x=y atunci 2\sqrt{xy}=x+y; si invers daca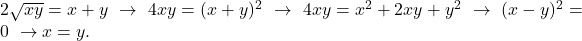 2\sqrt{xy}=x+y\ \rightarrow\ 4xy=(x+y)^2\ \rightarrow\ 4xy=x^2+2xy+y^2\ \rightarrow\ (x-y)^2=0\ \rightarrow x=y.

    Cum se demonstreaza acest lucru pentru egalitatea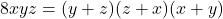 8xyz=(y+z)(z+x)(x+y). Rezulta asta in vreun fel din propozitia similara pentru inegalitatea mediei, de mai sus. Pentru ca risc sa cred ca este mai simplu sa arat ca 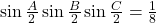\sin\frac{A}{2}\sin\frac{B}{2}\sin\frac{C}{2}=\frac18 daca si numai daca fiecare sinus este \frac12.

Raspunde

Raspunde