Aratati ca (m*n+n*p+p*m)^ 2 ≥ 3*m*n*p(m+n+p), ∀ m,n,p ∈ R
Sa se demonstreze ca daca x,y,z sunt numere reale pozitive si nenule ,avem inegalitatea
(x+y)^4/z + (y+z)^4 /x + (z+x)^4 /y ≥ 48 *x*y*z .
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Aratati ca (m*n+n*p+p*m)^ 2 ≥ 3*m*n*p(m+n+p), ∀ m,n,p ∈ R
Sa se demonstreze ca daca x,y,z sunt numere reale pozitive si nenule ,avem inegalitatea
(x+y)^4/z + (y+z)^4 /x + (z+x)^4 /y ≥ 48 *x*y*z .
Aratati ca (m*n+n*p+p*m)^ 2 ≥ 3*m*n*p(m+n+p), ∀ m,n,p ∈ R
La prima cerinta am ajuns la relatia
(mn)^2 +( np)^2+(pm)^2 ≥ mnp(m+n+p)
apoi
m^2n(n-p)+n^2p(p-m)+p^2m(m-n)≥0
sper sa nu fi gresit …
Aceste probleme imi par foarte cunoscute. Daca nu ma insel au fost date intr-un an la concursul interjudetean „Cristian Calude”.
CONTINUAREA SOLUTIEI DUMNEAVOASTRA: In inegalitatea: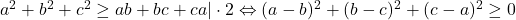
, adevarata, punem 
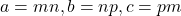si obtinem:
ALTFEL,DIRECT: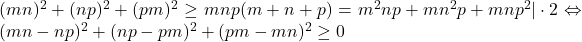
, adevarat.
multumesc!
Cuu cea mai mare placere!
P.S. Cred ca acolo unde se fac patratele ar fi indicat sa scrieti si pasii, adica sa grupati putin termenii.
Multa bafta!