Home/ Intrebari/Q 74780
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

andrei_g
Pe: 2011-11-30T14:15:07+02:00 In: In:

Ecuatii irationale

1. Sa se determine x real pt. care are loc egalitatea:

    \[ \sqrt[{3x - 1}]{{\sqrt[{8 - 3x}]{{( - x)^x }}}} = \sqrt[{5x}]{{2x}} \]

2.Sa se determine x si y numere reale pt. care:

    \[ 3\sqrt {x + y} + 2\sqrt {8 - x} + \sqrt {6 - y} = 14 \]

Similare

3 raspunsuri

  1. PhantomR
    expert (VI)

    1. Din conditiile de existenta:

    3x-1\in\mathbb{N^*} \Rightarrow 3x\in\mathbb{N} \rm{ si } 3x-1 \geq 1 \Leftrightarrow 3x \geq 2 \Leftrightarrow x\geq \frac{2}{3} \Rightarrow x\in\{\frac{p}{3};p\in\mathbb{N}, p \geq 2\}\\8-3x \in\mathbb{N^*} \Rightarrow 8-3x \geq 1 \Rightarrow x\leq \frac{7}{3} \Rightarrow x\in \{\frac{p}{3};p\in\mathbb{N^*}, 2 \leq p \leq 7\}.

    5x\in\mathbb{N^*} \Rightarrow x\in\{\frac{q}{5};q\in\mathbb{N^*}\}.

    Pentru a reduce putin numarul de incercari, sa intersectam cele doua multimi. Fie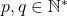 p,q\in\mathbb{N^*}: \frac{q}{5}=\frac{p}{3} \Leftrightarrow 3q=5p \Rightarrow p=M_{3}.

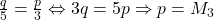    Asadar eventualele solutii sunt: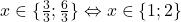 x\in\{\frac{3}{3};\frac{6}{3}\} \Leftrightarrow x\in\{1;2\}. Prima ar implica ca sub al doilea radical din membrul stang sa avem un numar negativ, imposibil. Asdar ramane de incercat x=2, care este intr-adevar o solutie.

    2. Din inegalitatea Cauchy-Buniakowski-Schwarz obtinem: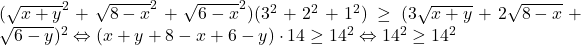 (\sqrt{x+y}^2+\sqrt{8-x}^2+\sqrt{6-x}^2)(3^2+2^2+1^2) \geq (3\sqrt{x+y}+2\sqrt{8-x}+\sqrt{6-y})^2 \Leftrightarrow (x+y+8-x+6-y)\cdot 14 \geq 14^2 \Leftrightarrow 14^2\geq 14^2, adica avem egalitate si obtinem din conditia de egalitate: 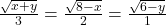\frac{\sqrt{x+y}}{3}=\frac{\sqrt{8-x}}{2}=\frac{\sqrt{6-y}}{1} sau prin ridicare la patrat: 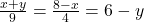\frac{x+y}{9}=\frac{8-x}{4}=6-y. Din ultimele doua obtinem: 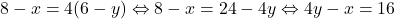8-x=4(6-y) \Leftrightarrow 8-x=24-4y \Leftrightarrow 4y-x=16, iar din primele doua obtinem: 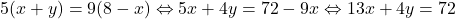5(x+y)=9(8-x) \Leftrightarrow 5x+4y=72-9x \Leftrightarrow 13x+4y=72. Rezolvam acum sistemul: 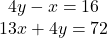\begin{matrix}4y-x=16 \\ 13x+4y=72\end{matrix} si eventual se va obtine solutia 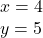x=4 \\ y=5. Prin verificare, aceasta este intr-adevar o solutie (satisface conditiile de existenta ale radicalilor si bineinteles si ecuatia propriu-zisa).

  2. andrei_g

    Multumesc mult si daca se poate sa pun o mica intrebare:
    La 1). cum se pun acele conditii? nu se pun acelea ca :

        \[ \sqrt[n]{a} \]

    , n>=2??

  4. PhantomR
    expert (VI)

    Cu cea mai mare placere!

    Din cate stiu eu, ordinul unui radical trebuie sa fie un numar natural. Eu am luat si posibilitatea ca acesta sa fie unu, dar probabil corect este cum ati spus dumneavoastra,adica sa se porneasca de la doi.

Raspunde

Raspunde