Home/ Intrebari/Q 74073
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

donny
Pe: 2011-10-22T15:38:20+03:00 In: In:

Partea intreaga

Demonstrati ca:

    \[\left[ x \right] + \left[ y \right] < \left[ {x + y} \right]\]

Va rog daca ma poate ajuta cineva.

Similare

10 raspunsuri

  1. PhantomR
    expert (VI)

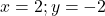    Pentru x=2;y=-2 avem egalitate, iar in cerinta inegalitatea este stricta. Te rog sa mentionezi restrictiile de variabile.

  2. andu_flavius95
    maestru (V)

        \[ \begin{array}{l} Corect\;este\;asa\;] \ge \left[ x \right] + \left[ y \right]\;,(\forall )x,y \in R \\ Dem: \\ Scriem\;x\;si\;y\;astfel:x = \left[ x \right] + \left\{ x \right\}\;si\;y = \left[ y \right] + \left\{ y \right\}\;,0 \le \left\{ x \right\} < 1\;si\;0 \le \left\{ y \right\} < 1 \\ \Rightarrow x + y = \left[ x \right] + \left[ y \right] + \left\{ x \right\} + \left\{ y \right\} \\ \Rightarrow \left. \begin{array}{l} x + y \ge \left[ x \right] + \left[ y \right] \\ \left[ x \right] + \left[ y \right] \in Z \\ \end{array} \right\} = > \left[ {x + y} \right] \ge \left[ x \right] + \left[ y \right] \\ \end{array} \]

  4. PhantomR
    expert (VI)

    O alta demonstratie adaptata dupa solutia de mai sus (sper sa nu fie identica.. adevarul e ca nu m-am prins de ce rezulta inegalitatea din ultimele doua afirmatii (cele cu acolada) ):

    x=[x]+\{y\} \\ y=[y]+\{y\} \Rightarrow x+y=[x]+[y]+\{x\}+\{y\} \Rightarrow [x+y]=[[x]+[y]+\{x\}+\{y\}]. Folosind proprietatea partii intregi: [a+k]=[a]+k,\forall a\in\mathbb{R},k\in\mathbb{Z} obtinem: [x+y]=[x]+[y]+[\{x\}+\{y\}] si inegalitatea devine:

    [x+y]=[x]+[y]+[\{x\}+\{y\}] \geq [x]+[y] \Leftrightarrow [\{x\}+\{y\}] \geq 0. Cum \{x\},\{y\} \in [0,1) avem: \{x\}+\{y\} \in [0,2), de unde rezulta [\{x\}+\{y\}] \in \{0,1 \}. Egalitatea are loc \Leftrightarrow \{x\}+\{y\} \in [0,1)

  5. J3anina
    maestru (V)

    PhantomR wrote: adevarul e ca nu m-am prins de ce rezulta inegalitatea din ultimele doua afirmatii (cele cu acolada) )


    Rezulta inegalitatea pentru ca, daca am avea x=1,5 si y=1,6 atunci
    [x+y]=[3,1]=3
    [x]+[y]=[1,5]+[1,6]=1+1=2

    Nota: exista posibilitatea ca {x} sau {y} >=0,5 si atunci {x}+{y}=1,…

  6. Bogdan Stanoiu
    maestru (V)

    PhantomR wrote: Pentru x=2;y=-2 avem egalitate, iar in cerinta inegalitatea este stricta. Te rog sa mentionezi restrictiile de variabile.


    In general daca {x}+{y}<1 avem ca
    [X+y]=[x]+[y] iar daca {x}+{y}>_1 avem ca
    [x+y]=[x]+[y]+1

    Mai general, daca n este un numar natural nenul si x(1);x(2);…;x(n) sunt numere reale atunci
    [x(1)+x(2)+…+x(n)]>_[x(1)]+[x(2)]+…+[x(n)], mai precis
    [x(1)+x(2)+….+x(n)]-([x(1)]+[x(2)]+…+[x(n)])=
    =[{x(1)}+{x(2)}+…+{x(n)}] care poate lua valori naturale de la 0 pana la n-1

  8. andu_flavius95
    maestru (V)

    PhantomR wrote: O alta demonstratie adaptata dupa solutia de mai sus (sper sa nu fie identica.. adevarul e ca nu m-am prins de ce rezulta inegalitatea din ultimele doua afirmatii (cele cu acolada) ):

    Cred ca ai inteles acum PhantomR, a spus J3anina mai sus . Scuze ca nu am explicat in rezolvarea initiala.

  9. J3anina
    maestru (V)

    Bogdan Stanoiu, da-mi si mie o idee la:

    te rog mult.

  10. PhantomR
    expert (VI)

    Aa.. cred ca m-am prins. Multumesc mult, J3anina si andu_flavius95!

  12. donny

    Va multumesc foarte mult!

  13. PhantomR
    expert (VI)

    Cu multa placere ! >:D<

Raspunde

Raspunde