Intr-un triunghi oarecare ABC, consideram punctele D,E,F,M astfel incat:
![]()
si
![]()
. (toti sunt vectori) Sa se arate ca punctele C,F,M sunt coliniare.
Multumesc mult
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Asadar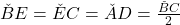 , iar din
, iar din 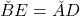 reiese ca
reiese ca 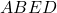 este paralelogram
este paralelogram 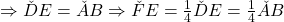 .
.
Tot din ipoteza avem si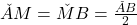 .
.
Deci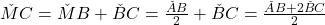 .
.
In concluzie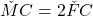 , adica vectorii
, adica vectorii 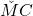 si
si 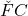 sunt coliniari, de unde rezulta apoi ca punctele
sunt coliniari, de unde rezulta apoi ca punctele 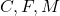 sunt coliniare.
sunt coliniare.
Observatie: PUnctul este deasemenea mijlocul segmentului
este deasemenea mijlocul segmentului ![Rendered by QuickLaTeX.com [MC]](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-1f79e21356b1176c2908ab0268a00e21_l3.png) .
.
Multumesc foarte mult.🙂
Cu multa placere!:)
O scurta nota in legatura cu vectorii: Daca vectorii au un punct comun (sau de intersectie) (exemplu: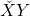 si
si 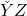 il ai un comun pe
il ai un comun pe 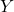 ), atunci daca exista
), atunci daca exista 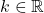 astfel incat
astfel incat 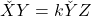 acesti doi vectori sunt coliniari sau paraleli. Spunem ca sunt coliniari (in adevaratul sens al cuvantului) din cauza acelui punct comun care arata ca ei nu pot fi paraleli.
acesti doi vectori sunt coliniari sau paraleli. Spunem ca sunt coliniari (in adevaratul sens al cuvantului) din cauza acelui punct comun care arata ca ei nu pot fi paraleli.