Am o serie de integrale duble, de nivelul anului I de facultate, interesante ca modalitate de calcul. Puteti sugera rezolvari.
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Iata o rezolvare pentru primul si ultimul subiect (la care nu am folosit coordonatele polare, deoarece mi s-a parut mai usor sa folosesc o schimbare de variabila). Daca ai nelamuriri in ceea ce priveste rezolvare, nu ezita sa intrebi.
Sper sa revin si cu rezolvarile celorlalte exercitii! Bafta la mariri/restante!
la umtima problema nu se vede primul rand, unde trebuia sa fie: xy=p
Iata si o rezolvare pentru 6.
Apropo, am uitat sa precizez, acolo unde s-au folosit coordonate polare ( x=r*cos(fi), y=r*sin(fi) ) avem restrictie ca r sa apartina [0,infinit) si fi sa apartina [0,2Pi]. Doar ca ele trebuiesc particularizate dupa caz (intersectate cu ceea ce ne intereseaza pe noi).
Multumesc foarte mult pentru rezolvari, J3anina.
Rezolvarea problemei 6 se presupune a fi facuta fara coordonate polare, iar rezultatul (care este dat) trebuie sa fie 1. 😆
incearca sa mai faci odata calculele, s-ar putea sa fi gresit eu pe la ele. oricum am sa ma mai uit si peste restul, poate o sa mai reusesc sa rezolv ceva.
Iara si o rezolvare pentru restul… Sper sa iti fie de ajutor
La problema 2, ln(0)= – infinit.. Si nu are cum sa dea asa ceva… Probabil nu am ales corect modalitatea de rezolvare… Nu am nici cea mai mica idee… mai intreaba pe cineva, poate o sa iti dea o alta idee.
Pentru 6 am reusit sa gasesc greseala. Eu practic am calculat: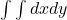 . Am uitat ca aveam de calculat:
. Am uitat ca aveam de calculat: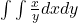 .
.
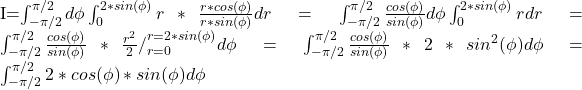 [tex]
[tex]
Ducand calculul pana la capat, intr-un mod surprinzator sau nu, am obtinut 0. Iata cum:
=\int_{-\pi/2}^{\pi/2}2*cos(\phi)*[-cos(\phi)]`d\phi=-2*\frac{cos^{2}(\phi)}{2}/_{\phi=-\pi/2}^{\phi=\pi/2}=-cos^{2}(\phi)/_{\phi=-\pi/2}^{\phi=\pi/2}=0![Rendered by QuickLaTeX.com [-cos(\phi)]`d](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-8b708d88edf9050bfbca9881132e7949_l3.png) ar trebui sa fie -cos(fi) derivat (ultimul rand, inainte de al 3-lea egal).
ar trebui sa fie -cos(fi) derivat (ultimul rand, inainte de al 3-lea egal).
[/tex].
Unde apare
Capetele de integrare si coordonatele polare, raman valabile de la calculul anterior.