Home/ Intrebari/Q 72566
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

andreea b
Pe: 2011-05-30T13:04:44+03:00 In: In:

trigooooooooo!

2.Sa se arate ca daca in triunghiul ABC avem:
a). A=2B , atunci a^2 – b^2 = bc

3.Sa se arate ca triunghiul ABC in care are loc relatia: sinA+ sinB=cosA+ cosB este dreptunghic.

Similare

1 raspuns

  1. PhantomR
    expert (VI)

    MASURILE DE UNGHIURI SUNT IN GRADE!

    2.a)

    \angle{A}=2\angle{B} (1). Aratam ca: a^2-b^2=bc.

    Din teorema Sinus: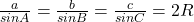 \frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R

    \angle{A}=2\angle{B} \Rightarrow \sin{A}=\sin{2B}=2\sin{B}\cos{B}

    Inlocuind apoi in teorema Sinus obtinem:

    \frac{a}{2\sin{B}\cos{B}}=\frac{b}{\sin{B}}. Deoarece \sin{B}\neq0 (contrariul ar implica \angle{B}=0 sau \angle{B}=180,imposibil), inmultim cu \sin{B} \Rightarrow 2b\cos{B}=a. Din teorema Cosinus avem: \cos{B}=\frac{a^2+c^2-b^2}{2ac}. Rezulta: 2b\frac{a^2+c^2-b^2}{2ac}\Leftrightarrow ba^2+bc^2-b^3=a^2c \Leftrightarrow bc^2-b^3=a^2c-ba^2 \Leftrightarrow b(c^2-b^2)=a^2(c-b) \Leftrightarrow b(c-b)(c+b)=a^2(c-b) \Leftrightarrow a^2(c-b)-(c-b)(bc+b^2)=0 \Leftrightarrow (c-b)(a^2-b^2-bc)=0 \Leftrightarrow c-b=0\Leftrightarrow b=c SAU a^2-b^2-bc=0 \Leftrightarrow a^2-b^2=bc.

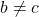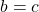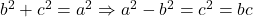    Daca b \neq c cerinta este demonstrata.Daca b=c atunci \bigtriangleup{ABC} este isoscel cu baza [BC][tex]\Rightarrow A=2B=2C \Rightarrow A+B+C=180 = 5B=5C \Rightarrow B=C=45 \Rightarrow A=90 \Rightarrow \bigtriangleup{ABC}[/tex] dreptunghic (si isoscel) si, din teorema lui Pitagora avem b^2+c^2=a^2 \Rightarrow a^2-b^2=c^2=bc. Cerinta este demonstrata.

    3. (revin mai tarziu) EDIT: Imi cer scuze de intarziere. Am scris rezolvarea acum cateva zile dar am inchis pagina din greseala si nu am mai rescris-o.

    sinA+sinB=cosA+cosB. Folosim transformarea sumelor in produse \Rightarrow

    sinA+sinB=2\sin\frac{A+B}{2}\cos\frac{A-B}{2}
    cosA+cosB=\cos\frac{A+B}{2}\cos\frac{A-B}{2}
    \Rightarrow 2\sin\frac{A+B}{2}\cos\frac{A-B}{2}=2\cos\frac{A+B}{2}\cos\frac{A-B}{2}|:2\cos\frac{A-B}{2} \Rightarrow \sin\frac{A+B}{2}=\cos\frac{A+B}{2} \Rightarrow \sin\frac{A+B}{2}-\cos\frac{A+B}{2}=0 . Ridicand aceasta ultima relatie la patrat \Rightarrow (\sin\frac{A+B}{2}-\cos\frac{A+B}{2})^2=0^2=0 \Rightarrow \sin^2\frac{A+B}{2}-2\cdot\sin\frac{A+B}{2}\cdot\cos+\frac{A+B}{2}+\cos^2\frac{A+B}{2}=0. Cum \sin^2\frac{A+B}{2}+\cos^2\frac{A+B}{2}=1 \Rightarrow 2\cdot\sin\frac{A+B}{2}\cdot\cos+\frac{A+B}{2} = 1 \Rightarrow \sin{A+B}=1 . Deoarece A+B<180 => A+B=90 \Rightarrow C=180-(A+B)=180-90=90, adica triunghiul ABC este dreptunghic in C, ceea ce trebuia demonstrat.

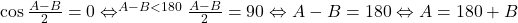    NOTE: \cos\frac{A-B}{2}=0 \Leftrightarrow^{A-B<180} \frac{A-B}{2}=90 \Leftrightarrow A-B=180 \Leftrightarrow A=180+B ,imposibil caci 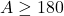A\geq180 ar implica A+B+C>180. In concluzie se poate imparti/inmulti cu \cos\frac{A-B}{2}\neq0 .

    2\sin{x}\cos{x}=\sin{2x} .

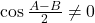    Sper ca am fost de ajutor si/sau ca nu am gresit pe undeva!

Raspunde

Raspunde