Demonstratie si explicare daca se poate.
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Problema a fost rezolvata in forum, cauta putin si ai s-o gaseste.
am cautat inainte sa postez… imi poti da un link? sau sub ce denumire e postata ?
Nu mai stiu unde a fost postata dar te asigur ca asa-i si chiar problema asta a fost ceruta pt rezolvare(si rezolvata)+celelalte, daca imi permite timpul am sa-ti-le caut.🙂
problema e ca nu prea stiu,sunt incepator si am nevoie de ea pt facultate.
te folosesti putin de http://en.wikipedia.org/wiki/Taylor_series:
ai asa dezvoltarea lu’ este
este  (te las pe tine sa demonstrezi, e simplu)
(te las pe tine sa demonstrezi, e simplu)  .
. (1) Pe de alta parte solutiile ecuatiei  sunt de forma
sunt de forma  cu n natural. Deci polinomial vorbind putem descompune pe
cu n natural. Deci polinomial vorbind putem descompune pe  astfel:
astfel: 
 din termenul drept este egal cu
din termenul drept este egal cu 
(2) . Dar conform (1) , coeficientul lui  este
este 
(3) deci din (1) si (3) obtinem egalitatea 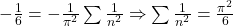
Acum, coeficientul lui
q.e.d.
m-ai salvat,mai am vreo 2-3 demonstratii postate pe forum,daca m-ati putea ajuta,as fi foarte recunoascator.Multam
celelalte cred ca sunt mai dificile. oricum incearca si tu prin metode asemanatoare poate-ti ies, mie mi-e lene sa-mi bat capu
alta demonstratie: te folosesti de http://mathworld.wolfram.com/ParsevalsTheorem.html la serii Fourier.
Consideri functia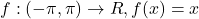 de unde calculezi si tu seria fourier si o sa-ti dea
de unde calculezi si tu seria fourier si o sa-ti dea  si acum folosesti teorema aia a lu Parseval si obtii ca
si acum folosesti teorema aia a lu Parseval si obtii ca  de unde itii iese imediat ca
de unde itii iese imediat ca 
q.e.d.
Uite si linku’ cu problemele cerute:http://forum.matematic.ro/viewtopic.php?t=3946;
Ideea este daca inlocuiesti x cu 1,2… obtii intocmai sumele cerute.Acesta este un alt mod de rezolvare a problemei, celelalte solutii au fost date de Gigi.
Ce ciuda imi e ca nu afiseaza .Era o rezolvare faina cu metode clasice de limite fara TAylor dar cam kilometrica.
Am intervenit eu, si am „reparat” astfel incat demonstratia dvs sa fie afisata.
Va sfatuiesc ca pe viitor, pentru a a evita astfel de necazuri, sa nu mai editati toata rezolvarea intr-o singura „formula” (adica un singur cod tex) ci sa o rupeti in mai multe. Evitati folosirea tabelelor, pentru ca acestea in gneral nu sunt afisate corespunzator pe site-ul nostru.
Eventual, pentru rezolvai lungi, scrieti intr-un alt editor, salvati ca fisier si atasati-l.
Foarte interesanta demonstratia