Determinați parametrul real a pentru care funcția este primitivabilă pe .
Nu prea știu cum ar trebui să abordez această problemă.. Oare ați putea să mă ajutați puțin?
AniDeȘcoală.ro Latest Intrebari
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Determinați parametrul real a pentru care funcția este primitivabilă pe .
Nu prea știu cum ar trebui să abordez această problemă.. Oare ați putea să mă ajutați puțin?
Orice functie care admite primitive este continua aproape peste tot, sau altfel spus o functie care are un numar infinit de puncte de discontinuitate nu admite primitive. Vom cauta a-urile pentru care functia are un numar infinit de puncte de discontinuitate.
O definitie a continuitatii spune ca o functie este continua in
daca pentru orice sir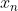 
care converge la 
, )
converge la )
.
Fie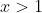
. Atunci exista un sir 
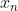de numere rationale si un sir 
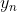de numere irationale care converg la 
.=\lim_{n\to\infty}\ln(e^{x_{n}}+a^2)=\ln(e^{x}+a^2))
. Analog, deoarece y este un sir de numere irationale, rezulta ca=\lim_{n\to\infty}\frac{1}{e^{y_{n}}}\ln(e^{y_{n}^2}+a^2)=\frac1{x}\ln(e^{x^2}+a^2))
Deoarece x este un sir de numere rationale rezulta ca
Trebuie sa vedem pentru care a-uri aceste 2 valori sunt diferite. Observam mai intai ca pentru a=0, cele 2 valori sunt egale. De asemenea, inlocuind in definitia lui f pe a=0, obtinem ca f(x)=x, o functie care admite primitive. Din pacate n-am reusit sa demonstrez ca in rest cele 2 valori sunt diferite, dar sunt destul de convins de acest lucru. O sa ma mai gandesc maine la problema, eventual la o alta rezolvare. Poti citi aici despre o functie asemanatoare cu functia ta:https://proofwiki.org/wiki/Dirichlet_Function_is_Discontinuous.