Home/ Intrebari/Q 5770
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

mary-
10
Pe: 2021-03-14T18:43:39+02:00 In: In:

Sa se calculeze limita. _____________ Pentru început …

Sa se calculeze limita\lim_{x\rightarrow 1}\frac{(\sqrt x-1)(\sqrt[3]{x}-1)\cdots(\sqrt[n]{x}-1)}{(x-1)^{n-1}}.

_____________
Pentru început am facut schimbarea de variabilă: \sqrt[2\cdot 3\cdot 4\cdots n]{x}=t\Rightarrow x=t^{n!}
Am înlocuit și am obținut:
\lim_{t\to1}\frac{{(t^{3\cdot4\cdots n}-1)(t^{2\cdot4\cdots n}-1)}\cdots(t^{2\cdot3\cdots n}-1)}{(t^{n!}-1)^{n-1}}

Si de aici nu stiu cum ar trebui sa continui. Ma gândeam dacă cumva as desface numărătorul si sa îl ditribui fiecărei paranteze.. insa nu stiu ce as putea face de acolo.

Ceva idei? Mulțumesc!

Similare

2 raspunsuri

  1. Menim

    Substitutia aceea nu cred ca duce niciunde, cu toate ca elimina radicalii.

    Ideea de a desface si distribui numitorul este insa foarte buna. Observam ca la numarator avem n-1 paranteze(deoarece avem radical din 2 pana la n), iar puterea numitorului este tot n-1. Atunci este natural sa distribuim astfel numitorul:
    \lim_{x\to 1}\frac{(\sqrt{x}-1)(\sqrt[3]{x}-1)...(\sqrt[n]{x}-1)}{(x-1)^{n-1}}=\lim_{x\to 1}\frac{\sqrt{x}-1}{x-1}\cdot\frac{\sqrt[3]{x}-1}{x-1}...\frac{\sqrt[n]{x}-1}{x-1}.

    Termenii produsului sunt de forma \frac{\sqrt[n]{x}-1}{x-1} unde n este doar o constanta finita. De aceea limita produsului este produsul limitelor termenilor.

    Mai ramane sa calculam limita unui termen de aceasta forma. Cea mai usoara metoda este sa observam ca limita este de forma 0/0 si sa aplicam lHospital(tinand cont de faptul ca \sqrt[n]{x}=x^{\frac1{n}}):
    \lim_{x\to1}\frac{x^{\frac1{n}}-1}{x-1}=\lim_{x\to1}\frac1{n}x^{\frac1{n}-1}=\frac1{n}

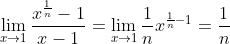
    Atunci limita noastra este pur si simplu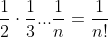 \frac12\cdot\frac13...\frac1{n}=\frac1{n!}.

Raspunde

Raspunde