Home/ Intrebari/Q 2016
Urmator
Answered

AniDeȘcoală.ro Latest Intrebari

matt727
15
Pe: 2020-07-12T21:02:02+03:00 In: In:

Inegalitate folosind teorema lui Lagrange ln(x)/(x+1)<ln^2(x+1)-ln^2(x)<ln(x+1)/x

Inegalitate folosind teorema lui Lagrange

ln(x)/(x+1)<ln^2(x+1)-ln^2(x)<ln(x+1)/x

Similare

9 raspunsuri

  1. Menim

    Ce se cere?

  3. matt727

    Trebuie demonstrat folosind teorema lui Lagrange

  4. matt727

    Am verificat daca este cum zici
    dar egalitatea este adevărată și pentru x>=e.

  6. matt727

    dav

    Acesta este ex complet din culegere.

  7. Menim
    Best Answer

    Enuntului initial ii lipsea un 2. Aceasta este inegalitatea de demonstrat:
    \frac{\ln x}{x+1}<\frac{\ln^2(x+1)-\ln^2x}2<\frac{\ln(x+1)}x

    Consideram functia f:[x, x+1]\to R, f(y)=\ln^2(y). Functia este continua si derivabila pe intervalul [x, x+1], avand derivata:
    f\prime(y)=2\cdot\frac{\ln y}{y}. Din Teorema lui Lagrange, exista cel putin un c din intervalul (x, x+1)  cu proprietatea ca:
    f\prime(c)=\frac{f(x+1)-f(x)}{(x+1)-x}
    Inlocuind f si f’, obtinem:
    2\cdot\frac{\ln c}{c}=\ln^2(x+1)-\ln^2(x)
    Impartim cu 2:
    \frac{\ln c}{c}=\frac{\ln^2(x+1)-\ln^2(x)}2
    Inegalitatea data devine:
    \frac{\ln x}{x+1}<\frac{\ln c}c<\frac{\ln(x+1)}x

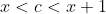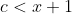    Deoarece c apartine intervalului (x, x+1), rezulta ca x<c<x+1. Logaritmul este o functie strict crescatoare, deci \ln(x)<\ln c. Din faptul ca c<x+1 rezulta prima parte a inegalitatii de mai sus.

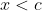    Tot din monotonia logaritmului avem ca \ln c<\ln(x+1). Din x<c rezulta si a 2-a parte a inegalitatii.

  8. matt727

    Acum am observat, îmi cer scuze. Mulțumesc frumos pentru ex!

Raspunde

Raspunde