Fie legea de compozitie
x*y=3(x-1/3)(y-1/3)+1/3
Sa se determine
1*1/√2*1/√3*…*1/√2021
AniDeȘcoală.ro Latest Intrebari
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Fie legea de compozitie
x*y=3(x-1/3)(y-1/3)+1/3
Sa se determine
1*1/√2*1/√3*…*1/√2021
Observam mai intai ca aceasta lege de compozitie este asociativa, adica*z=3(3(x-\frac13)(y-\frac13)+\frac13-\frac13)(z-\frac13)+\frac13=9(x-\frac13)(y-\frac13)(z-\frac13)+\frac13=3(x-\frac13)(3(y-\frac13)(z-\frac13)+\frac13-\frac13)+\frac13=3(x-\frac13)(y*z-\frac13)+\frac13=x*(y*z))
.
De asemenea, legea este comutativa:
(y-\frac13)+\frac13=3(y-\frac13)(x-\frac13)+\frac13=y*x)
.
Acum, cautam un numar/element a cu proprietatea c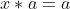a
adica (a-\frac13)+\frac13=a)
, de unde avem (a-\frac13)=a-\frac13)
. Se observa usor acum ca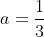 
este un asemenea element. Deoarece legea de compozitie este comutativa, avem si ca 
.
Cu aceste lucruri, expresia se calculeaza astfel:
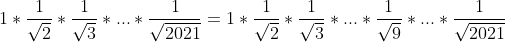
Din asociativitate:
*\frac1{\sqrt9}*(\frac1{\sqrt{10}}...*\frac1{\sqrt{2021}}))
Notand parantezele cu x si y:
*\frac1{\sqrt9}*(\frac1{\sqrt{10}}...*\frac1{\sqrt{2021}})=x*\frac1{\sqrt9}*y=x*\frac13*y)
In final aplicand proprietatea lui 1/3(termenul a ce l-am gasit mai sus), expresia este egala cu
.