Exercitiul E3 doar atat imi trebuie . Multumesc
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Exercitiul E3 doar atat imi trebuie . Multumesc
1.Functia exista si e continua pe tot intervalul dat fiind compunere de functii elementare. Derivata ei este=\frac{1}{2\sqrt{x-1}})
.)
, interval pe care este si continua din acelasi motiv ca mai sus.
Aceasta exista din cauza numitorului doar pe intervalul
2.Functia exista si e continua pe tot intervalul dat. Derivata sa este=\frac{e^{\sqrt{x}}}{2\sqrt{x}})
care exista din cauza numitorului doar pe intervalul )
pe care este si continua.
3.Functia se mai scrie si ca:
=\left\{\begin{matrix}&space;(x^2-1)^3\text{,&space;}x\leq-1\\&space;(1-x^2)^3\text{,&space;}x\in(-1,&space;1)\\&space;(x^2-1)^3\text{,&space;}x\geq1&space;\end{matrix}\right.)
=\left\{\begin{matrix}&space;3(x^2-1)^2\cdot2x\text{,&space;}x\leq-1\\&space;3(1-x^2)^2\cdot(-2x)\text{,&space;}x\in(-1,&space;1)\\&space;3(x^2-1)^2\cdot2x\text{,&space;}x\geq1&space;\end{matrix}\right.)
Functia este continua pe toate aceste intervale, si facand limitele laterale in capete se observa direct ca functia este continua pe tot intervalul dat.
Derivatele pe aceste intervale sunt:
Facand limitele laterale se observa ca toate sunt 0 deci derivata exista si e continua pe tot intervalul.
4.Functia se scrie ca:
=\left\{\begin{matrix}&space;\ln(1+e^{-x})\text{,&space;}x<0&space;\\\ln(1+e^x)\text{,&space;}x\geq0&space;\end{matrix}\right.)
=\left\{\begin{matrix}&space;\frac{-e^{-x}}{1+e^{-x}}\text{,&space;}x<0&space;\\\frac{e^x}{1+e^x}\text{,&space;}x\geq0&space;\end{matrix}\right.)
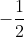iar de la dreapta este egala cu 
deci functia nu este derivabila in 0. Rezulta ca intervalul de derivabilitate este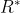 
.
Functia exista pe tot intervalul deoarece exponentiala este strict pozitiva si deci argumentul logaritmului va fi si el pozitiv. Limitele laterale sunt egale cu 0 deci functia este continua pe tot intervalul. Derivatele pe intervale sunt:
Limita laterala in 0 de la stanga este egala cu
5.Functia se scrie ca:
=\left\{\begin{matrix}&space;\arcsin(-x)\text{,&space;}x<0\\&space;\arcsin(x)\text{,&space;}x\geq0&space;\end{matrix}\right.=\left\{\begin{matrix}&space;-\arcsin(x)\text{,&space;}x<0\\&space;\arcsin(x)\text{,&space;}x\geq0&space;\end{matrix}\right.)
=\left\{\begin{matrix}&space;\frac{-1}{\sqrt{1-x^2}}\text{,&space;}x<0\\&space;\frac1{\sqrt{1-x^2}}\text{,&space;}x\geq0&space;\end{matrix}\right.)
.
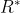Limitele laterale sunt ambele egale cu 0, deci functia este continua pe tot intervalul. Derivatele pe intervale sunt:
Limitele laterale sunt egale cu -1 si 1, deci functia este derivabila pe
6.Functia se rescrie ca:
=\left\{\begin{matrix}&space;\arccos(-x)\text{,&space;}x<0\\&space;\arccos(x)\text{,&space;}x\geq0&space;\end{matrix}\right.)
=\left\{\begin{matrix}&space;\frac1{\sqrt{1-x^2}}\text{,&space;}x<0\\&space;-\frac1{1-x^2}\text{,&space;}x\geq0&space;\end{matrix}\right.)
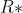
Limitele laterale sunt egale deci functia este continua pe R. Derivatele sunt:
Ca la 5, limitele laterale nu sunt egale deci functia e derivabila doar pe