Exercitiile 3 si 4. Am incercat cu definitia functiilor continue si nu mi a iesit.
AniDeȘcoală.ro Latest Intrebari
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Exercitiile 3 si 4. Am incercat cu definitia functiilor continue si nu mi a iesit.
O functie e continua in n daca limitele sale laterale sunt egale intre ele si egale cu valorile functiei. Sa calculam limita din stanga:
![\lim_{x\to n, x<n}g(x)=\lim_{x\to n, x<n}[x]\cdot\lim_{x\to n, x<n}f(x)](https://latex.codecogs.com/gif.latex?\lim_{x\to&space;n,&space;x<n}g(x)=\lim_{x\to&space;n,&space;x<n}[x]\cdot\lim_{x\to&space;n,&space;x<n}f(x))
Prima limita este egala cu n-1 din definitia partii intregi(de exemplu daca n=5 si facem limita cand x tinde la n si x<5, atunci de exemplu x poate fi egal cu 4.99, caz in care partea sa intreaga este 4, adica n-1).
A 2-a limita este egala cu f(n) deoarece stim ca f este o functie continua. Atunci limita este egala cuf(n))
.
Dar deoarece functia g este continua, limita sa laterala stanga este egala cu valoarea functiei in n, deci:
f(n)=nf(n))
-f(n)=nf(n))
=0)
Deci f este functia nula.
Avem-f(\frac{x}{e})=x)
. Notand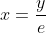 
, obtinem ca -f(\frac{y}{e^2})=\frac{y}{e})
si revenind la variabila x, avem -f(\frac{x}{e^2})=\frac{x}{e})
.
Continuand in acelasi mod obtinem ca-f(\frac{x}{e^n})=\frac{x}{e^{n-1}})
. Scriem aceasta relatie de la 1 la n, adica:
-f(\frac{x}{e})=x)
-f(\frac{x}{e^2})=\frac{x}{e})
-f(\frac{x}{e^3})=\frac{x}{e^2})
-f(\frac{x}{e^n})=\frac{x}{e^{n-1}})
.
.
.
Adunam aceste relatii:
-f(\frac{x}{e})+f(\frac{x}{e})-f(\frac{x}{e^2})+f(\frac{x}{e^2})-f(\frac{x}{e^3})+...+f(\frac{x}{e^{n-1}})-f(\frac{x}{e^n})=x+\frac{x}{e}+\frac{x}{e^2}+...+\frac{x}{e^{n-1}})
-f(\frac{x}{e^n})=x(1+\frac1{e}+\frac{1}{e^2}+...+\frac{1}{e^{n-1}}))
Observam ca in partea stanga toti termenii se anuleaza mai putin primul si ultimul. In dreapta dam factor comun pe x:
Inmultim aceasta expresie cu e:
-f(\frac{x}{e^n}))=x(e+1+...+\frac{1}{e^{n-2}}))
Scadem expresia anterioara din aceasta:
(f(x)-f(\frac{x}{e^n}))=x(1+\frac1{e}+...+\frac{1}{e^{n-1}}-e-1-...-\frac1{e^{n-2}})=x(\frac1{e^{n-1}}-e))
Lasand n sa tinda la infinit, avem:
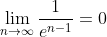si deoarece f este functie continua, =f(\lim_{n\to\infty}\frac{x}{e^n})=f(0)=\frac1e)
. Rezulta atunci ca:
(f(x)-\frac1e)=x(-e))
-\frac1e=\frac{-ex}{e-1})
=\frac{-ex}{e-1}+\frac1{e}=\frac{-e^2x+e-1}{e(e-1)})
Se poate observa, ca o verificare, ca valoarea lui f(0) este intr-adevar cea ceruta.