Home/ Intrebari/Q 92543
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

ana anuta
Pe: 2018-02-13T15:02:44+02:00 In: In:

trapez

STAR trapez is ortodiagonal. ST baza mare.O este punctul de intersectie al diagonalelor. Ducem MN prin O paralela la baze. B este mijl
AT. NB=BC, unde C este pe AT.Sa se dem ca m(\measuredangle
CMS)=90^{\circ} si SR=CM.
Dem. Ducem RH perpendicular pe ST. RH\capSO=Z=
ortocentrul SRT. Cred ca trebuie sa dem ca TZ paralel cu CM.
Stim ca RH = linia mijlocie. Rog ajutor. Multumesc.

Similare

2 raspunsuri

  1. ghioknt
    profesor

    Fie B, b lungimile celor două baze. Așa cum spui,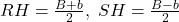 RH=\frac{B+b}{2},\;SH=\frac{B-b}{2},
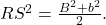
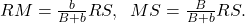
    în consecință, RS^2=\frac{B^2+b^2}{2}.
    Teorema fundamentală a asemănării spune că triunghiurile OAR și OST sunt asemenea, de unde OA/OS=b/B, deci și
    RM/MS=b/B. Prin proporții derivate: RM=\frac{b}{B+b}RS,\;\;MS=\frac{B}{B+b}RS.
    Pentru că C și T sunt simetricele lui N, respectiv, A față de mijlocul B, avem CT=AN, iar dacă ducem și CD paralelă cu bazele, avem RM=AN, MD=NC, DS=CT etc. MD=MS-CS=\frac{B-b}{B+b}RS.
    Nu e greu de demonstrat că lungimea unei paralele la baze, așa cum este CD, este medie aritmetică ponderată a numerelor B, b, cu ponderi proporționale cu lungimile RC, CS. Ori aceste lungimi sunt proporționale tocmai cu B, b (RC/CS=B/b), deci CD=\frac{B\cdot B+b\cdot b}{B+b}=\frac{B^2+b^2}{B+b}=\frac{RS^2}{RH}.
    Triunghiurile CDM și RSH au unghiurile din D și S congruente, dar și laturile alăturate acestor unghiuri, proporționale:
    \frac{MD}{SH}=\frac{(B-b)RS}{B+b}\cdot\frac{2}{B-b}=\frac{RS}{RH};\;\frac{CD}{RS}=\frac{RS^2}{RH}\cdot\frac{1}{RS}=\frac{RS}{RH}.
    Conform cazului de asemănare LUL, triunghiurile respective sunt asemenea. Asta înseamnă că și triunghiul CDM este dreptunghic (în M) iar cel de al treilea raport are aceeași valoare cu celelalte: \frac{CM}{RH}=\frac{RS}{RH}.

  2. ghioknt
    profesor

    Fie B, b lungimile celor două baze. Așa cum spui,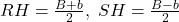 RH=\frac{B+b}{2},\;SH=\frac{B-b}{2},
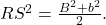
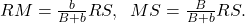
    în consecință, RS^2=\frac{B^2+b^2}{2}.
    Teorema fundamentală a asemănării spune că triunghiurile OAR și OST sunt asemenea, de unde OA/OS=b/B, deci și
    RM/MS=b/B. Prin proporții derivate: RM=\frac{b}{B+b}RS,\;\;MS=\frac{B}{B+b}RS.
    Pentru că C și T sunt simetricele lui N, respectiv, A față de mijlocul B, avem CT=AN, iar dacă ducem și CD paralelă cu bazele, avem RM=AN, MD=NC, DS=CT etc. MD=MS-CS=\frac{B-b}{B+b}RS.
    Nu e greu de demonstrat că lungimea unei paralele la baze, așa cum este CD, este medie aritmetică ponderată a numerelor B, b, cu ponderi proporționale cu lungimile RD, DS. Ori aceste lungimi sunt proporționale tocmai cu B, b (RD/DS=B/b), deci CD=\frac{B\cdot B+b\cdot b}{B+b}=\frac{B^2+b^2}{B+b}=\frac{RS^2}{RH}.
    Triunghiurile CDM și RSH au unghiurile din D și S congruente, dar și laturile alăturate acestor unghiuri, proporționale:
    \frac{MD}{SH}=\frac{(B-b)RS}{B+b}\cdot\frac{2}{B-b}=\frac{RS}{RH};\;\frac{CD}{RS}=\frac{RS^2}{RH}\cdot\frac{1}{RS}=\frac{RS}{RH}.
    Conform cazului de asemănare LUL, triunghiurile respective sunt asemenea. Asta înseamnă că și triunghiul CDM este dreptunghic (în M) iar cel de al treilea raport are aceeași valoare cu celelalte: \frac{CM}{RH}=\frac{RS}{RH}.

    PS Am corectat greșelile din postarea precedentă, dar nu știu să o fac să dispară. Actualul site nu oferă posibilități de corectare pentru o postare mai veche sau nu știu eu să o fac.

Raspunde

Raspunde