Pe multimea G=(1,2)U(2,+infinit) se defineste legea de compozitie GxG–>G, (x,y)–> x compus cu y=(x-1)^ln(y-1)+1. G este sau nu parte stabila in raport cu legea data?
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Cum rezulta
rezulta 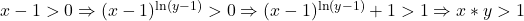
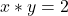 .
.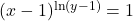
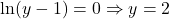 , contradictie.
, contradictie. , contradictie.
, contradictie.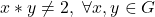
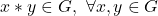 , deci G este parte stabila.
, deci G este parte stabila.
Presupunem ca ar exista x si y din G astfel incat
Atunci
Avem doua cazuri:
1. exponentul este egal cu 0. Atunci
2. baza puterii este egala cu 1. Rezulta
Deci
In concluzie,
Expresia exista daca x-1>=0 si y-1>0 si minimul expresiei estemai mare ca 1
Daca x=y=lim(t->0)[2±t]-vom avea x*y=lim(t->0)[(1±t)^ln(1±t) +1]-> e^0+1=2
erata[
Nu s-a tiparit,,deci multimea data G este parte stabila indusa de legea de compoziti data pe multimea M= (1,+inf)
Va multumesc!🙂
Întrebare greşit formulată. Întrebarea corectă ar fi: G este parte stabilă a mulţimii H=… în raport cu legea de compoziţie dată?
Legea de compoziţie trebuie dată pe mulţimea H.
Aici însă nu se dă nicio mulţime H, aşa că problema subînţeleasă este: să se determine o mulţime H astfel încât:
a) corespondenţa dată să fie lege de compoziţie pe H;
b) G să fie parte stabilă a lui H în raport cu legea de compoziţie pe H.
Sau, fără H, întrebarea putea fi: este G stabilă fată de legea dată?
Legea dată nu este o lege (funcţie?) oarecare, ci, aşa cum scrie negru pe alb în ipoteza problemei, este o lege de compoziţie pe G.
O lege de compoziţie pe G este, prin definiţie, o funcţie definită pe GXG, cu valori neapărat în G, aşa cum este întărit încă
odată în textul ipotezei problemei. Şi atunci, ce avem de demonstrat, ipoteza problemei?
Dacă vrem să nu aruncăm la coş această problemă, o putem reformula:
Fie G=(1; 2)U(2; oo) şi funcţia GXG–>R, (x,y)–>x*y=1+(x-1)^ln(y-1). Arătaţi că această funcţie este o lege de compoziţie pe G
(sau G este stabilă în raport cu legea de corespondenţă dată), plus, eventual, proprietăţile uzuale ale unei legi de compoziţie,
structura lui G, izomorfisme etc.