Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
846.Pe R se defineste legea de compozitie x*y=axy-x-y+2 , a,x,y din R
Multimea valorilor lui a, pt care intervalul [0,2] este parte stabila in raport cu legea „*” este
a.[0,1]
b.{1}
c.{0,2}
d.[0,2]
e.[1/2,1]
847.Multimea valorilor lui a pt care legea admite EN este?
848.Multimea valorilor lui a pt care ([0,2],*) este grup este?
Admitere UTCN 2015
Pentru a=0: 2*2=-2-2+2=-2 care nu este în [0; 2], deci cele 3 răspunsuri care conţin pe 0 sunt false.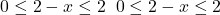
care, înmulţite între ele şi cu 1/2,
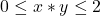, adică, pentru a=1/2, intervalul [0; 2] este parte stabilă a lui R.
Pentru a=1/2 legea de compoziţie se poate scrie şi x*y=(1/2)(x-2)(y-2) sau (1/2)(2-x)(2-y).
Pentru orice x, y din[0; 2] sunt adevărate inegalităţile
conduc la
Deci, între b. şi e. vom bifa pe e., singurul care îl conţine pe 1/2.
Dacă e este elementul neutru, atunci axe-x-e+2=x, sau (ae-2)x+2-e=0 pentru orice x real, şi sistemul 2-e=0, ae-2=0
conduce la e=2, a=1.
Dacă [0;2] este grup, atunci trebuie să aibă element neutru, care nu poate fi decât 2 şi numai dacă a=1.
Scriind că simetricul lui 1 este s: 1*s-1-s+2=2 imposibil, Deci [0; 2] nu poate fi grup.