Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Aratati ca functia nu este surjectiva:
f(x) = x^2 – 6x + 5
f surj<=>
Oricare y apartine R, exista x apartine R a.i. f(x)=y
As dori si eu un model de rezolvare..
Chiar nu inteleg ce ar trebui sa fac la f. de gr II
Cum negi propozitia: „Oricare y apartine R, exista x apartine R a.i. f(x)=y”?
f nu e surj <=>
exista y apartine B, oricare x apartine A, f(x) != y
dar nu inteleg ce trebuie sa fac…
sa zic ca fac cu delta si imi da valorile: x1=5 , x2=1
si apoi?
Priam parte e buna. Acum aplica la probema ta.
Cu ce te ajuta delta? Cum arata o functie de grad 2? Ce caracteristici stii tu in general despre un functie de grad 2?
Bun. Hai sa facem si cu delta.
x^2-6x+5-y=0. Vrem ca ecuatia asta sa nu aiba solutii.
Cand se intampla asta?
Nu stiu. Nu ma mai invartiti cu intrebari din acestea ca nu mai inteleg nimic.
Daca vreti sa ma ajutati bine, daca nu, nu…
Am cerut si eu un model pas cu pas sa vad cum se rezolva un exemplu..
Din postările tale deduc că tu ştii nişte texte, dar nu le înţelegi. Înţelegi un text dacă eşti în stare să-i redai conţinutul folosind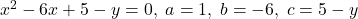
.
.
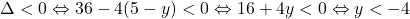şi alte cuvinte, adică dacă poţi să-l înlocuieşti cu un text matematic echivalent.
De exemplu, textul tău Oricare y apartine R, exista x apartine R a.i. f(x)=y este echivalent cu textul
Oricare y aparţine R, ecuaţia f(x)=y (cu necunoscuta x) are cel puţin o soluţie reală.
Iar textul tău exista y apartine B, oricare x apartine A, f(x) != y
este echivalent cu
există y aparţine R, a. î. ecuaţia f(x)=y nu are nicio soluţie în R (pentru că la tine A=B=R).
De ce acest text este mai ”breaz” decît precedentul? Pentru că, trebuie să recunoşti, despre ecuaţii ştii mult mai multe decât
laşi să se vadă în postările tale. De exemplu ecuaţia f(x)=y este de fapt ecuaţia de gradul II
Dacă vrei să nu aibă soluţii, trebuie să vezi dacă este posibil ca Delta<0.
Deci există y în R pentru care egalitatea f(x)=y nu se întâmplă.
Această rezolvare se bazează pe textele scrise de tine. Altă soluţie se poate baza pe graficul funcţiei f.
permiteti-mi sa vin si eu cu o idee.
Pentru a putea sa analizezi surjectivitatea unei functii trebuie precizat atat doneniul cat si codomeniul functii-f; A->B
Ex;functia f; Z->Z unde f=5x nu este surjectiva dar functia ; f;R->R unde f=5x este surjectiva