Exista o infinitate de patrate perfecte care sa inceapa cu 2016?
Banuiesc ca raspunsul este afirmativ (iar in loc de 2,0,1,6 puteau fi luate oricare cifre) dar nu am reusit sa dovedesc.
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Niste sugestii.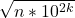 fata de
fata de  ?
?
1. Care este diferenta dintre 2 patrate perfecte consecutive?
2. Daca adaugam 2k zerouri la sfarsitul unui numar n, cu ce ordin de marime creste
1. Multumesc pentru dorinta de a ma ajuta; Stiu ca diferenta dinte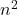 si
si 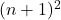 este
este  dar nu vad cum ma pot folosi de acest lucru
dar nu vad cum ma pot folosi de acest lucru
2. Inteleg ca ati luat un numar oarecare in locul lui 2016 dar acum, pentru a arata ca exista un patrat perfect care sa inceapa cu
in locul lui 2016 dar acum, pentru a arata ca exista un patrat perfect care sa inceapa cu  nu inteleg la ce mi-ar folosi ideea dvs pentru ca eu consider ca ceea ce trebuie sa facem este sa argumentam existenta unui patrat perfect cuprins intre
nu inteleg la ce mi-ar folosi ideea dvs pentru ca eu consider ca ceea ce trebuie sa facem este sa argumentam existenta unui patrat perfect cuprins intre 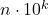 si
si 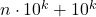 .
.
Nu degeaba am pus 2k zerouri la sfarsitului numarului n.![Rendered by QuickLaTeX.com \sqrt{n}<\left [\sqrt{n}\right ]+1 \Rightarrow \sqrt{n*10^{2k}}<10^k*(\left [\sqrt{n}\right ]+1)](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-f24ff22fce7337460505aefedbced812_l3.png) .
.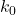 astfel incat
astfel incat ![Rendered by QuickLaTeX.com 2*(10^k*(\left [\sqrt{n}\right ]+1))+1 \le 10^{2k}, \forall k>k_0](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-cc1f48dd7d4554e534031f265447da24_l3.png) .
.
Avem:
Trebuie sa mai demonstram ca exista un
Care este sursa problemei?
In culegrea „BAC 2004” aparuta la Editura GIL se cere valoarea de adevar a propozitiei „o infinitate de patrate perfecte incep cu cifrele 2,0,0,3”
Patratul lui![Rendered by QuickLaTeX.com {10^k} \cdot \left( {\left[ {\sqrt n } \right] + 1} \right)](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-da8b2a52d3aec347a636397c5ce9d4a1_l3.png) nu are la inceput cifrele numarului
nu are la inceput cifrele numarului  , de exemplu pentru
, de exemplu pentru 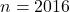 avem
avem ![Rendered by QuickLaTeX.com \left[ {\sqrt {2016} } \right] + 1 = 45](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-ba835493e2efc7c6cf8fb62267657e65_l3.png) iar
iar 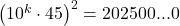 nu incepe cu cifrele 2,0,1,6.
nu incepe cu cifrele 2,0,1,6.
Am observat ca daca as demonstra capentru orice numar natural nenul n exista cel putin un patrat perfect care incepe cu cifrele numarului n atunci de aici ar rezulta imediat ca si consecinta ca exista o infinitate de astfel de patrate perfecte.
Ramane deci de demonstrat propozitia evidentiata!
Credeam ca urmaresti altceva. Din pacate vad ca n-ai inteles sugestiile mele.
Majorarile de acolo sunt pentru cu totul altceva. Si anume pentru a arata ca urmatorul patrat perfect intra in intervalul dorit. Si nu de a gasi un patrat perfect.
Altfel ti-as fi putut spune ca 20164 este patrat perfect si aici incheiam problema.
Nu ati inteles! Eu vreau sa demonstrez existenta unui numar nesfarsit de astfel de patrate
Intentia e justa, m-am prins de asta, dar nu vad cum s-ar finaliza demonstratia!
Nu ati inteles! Eu vreau sa demonstrez existenta unui numar nesfarsit de astfel de patrate
Din momentul in care stim ca 20164 este patrat perfect, putem construi o infinitate de patrate perfecte de forma 20164*10^{2k}.
Intentia e justa, m-am prins de asta, dar nu vad cum s-ar finaliza demonstratia!
Sper ca am dat destule indicatii pe PM pentru a intelege si finalizarea problemei.
Sa abandonam exemplul cu 2016 luand cazul general.
Din pacate, in a doua postare a dvs din acest topic nu ati pus asa cum ati intentionat parantezele partii intregi:
Dupa cele ce mi-ati scris pe PM am inteles ca de fapt daca luam![Rendered by QuickLaTeX.com x = \left[ {\sqrt {n \cdot {{10}^{2k}}} } \right]](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-ece806c411f3f40df6ea521e38b28e0f_l3.png) atunci
atunci 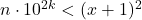 si este suficient sa demonstram ca exista k astfel incat
si este suficient sa demonstram ca exista k astfel incat
conditie care este asigurata daca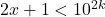 , adica
, adica
Caut sa vad mai departe cum argumentam existenta lui k care sa aiba aceasta proprietate!
Da, continuarea ar putea fi aceasta:
Deoarece
e suficient ca
relatie asigurata daca
Evident, exista astfel de valori k !
Multumiri domnului A_Cristian si acum vad ca parantezele din cea de a doua postare erau puse exact asa cum intentionase, doar ca se referea la pasul urmator celui in care ma aflam eu cu intelegerea problemei!