Fie sirul (In) unde n nr natural, In=integrala de la 0 la 1 din(x^n/3x+8)dx.
a)Sa se calculeze I2
b)Sa se arate ca 3In+1+8In=1/(n+1).
c)lim cand n tinde la infinit din n*In.
Am rezolvat cerintele a si b,dar la c nu ma descurc.
Multumesc frumos!!


punctul c:
http://i.imgur.com/vtKEAqd.png
dacă f e continuă în 1. Dacă e şi derivabilă, demonstraţia e imediată, folosind integrarea prin părţi.
A apărut de multe ori pe acest site.
@gunty: când trecem la limită, inegalităţile stricte devin nestricte.
@MaTe1997 Mi-e greu să înţeleg cum cineva care pare că pricepe ceva matematică nu face diferenţa între x^n/3x+8 şi x^n/(3x+8 ).
Va multumesc domnilor.Ideea este ca nu am facut inca anumite proprietati,doar ce am vazut din manual,probabil deaia nu am avut nici idee.Va doresc multa sanatate si un an nou plin de bucurie alaturi de cei dragi!!
P.S:Imi cer scuze pentru paranteza omisa,era 1:39 noaptea ora postarii,scriam de pe telefon…
In acest caz nu este vorba de integrala de la 0 la 1 ci de la 1 la n, deci observatia dumneavoastra nu functioneaza. Pe langa asta, eu am dedus din nI_n strcit crescator si nI_n>1/11 faptul ca lim(nI_n)>1/11, ceea ce mi se pare logic, deoarece e clar ca limita nu are cum sa fie 1/11 (avand in vedere ca sirul este strict crescator). Pentru a clarifica lucrurile mai bine, va invit sa vedeti ce valoare are sirul nI_n de exemplu pentru n=5:
http://tinyurl.com/h2pawlq
Are dreptate domnul gunty,daca era integrala de la (0,1) era cum spuneti dv.Dar avand in vedere ca e de la (1,n) este infinit.Toate cele bune!!
Cu siguranţă e o greşeală de scriere, şi integrala era pe [0,1]. Două motive: 1) dacă e pe [1,n], egalitatea de la punctul b) este falsă (şi a şi fost folosită în demonstraţia de mai sus).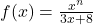 e crescătoare, deci
e crescătoare, deci 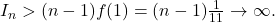
2) dacă e pe [1,n], limita de la c) e evident infinită, pentru că
Evident, şi nI_n va tinde la infinit.
Asa ne-a zis cerinta domnul profesor…Si e gresita,aveti dreptate domnule gigelmarga.Eu va multumesc inca o data din tot sufletul si imi cer scuze pentru deranjul facut.Multa sanatate si toate cele bune…😳