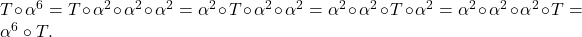Mi se da o permutare alfa α ce are pe linia I elementele : 1 2 3 4 5 si pe linia a II a elem. : 2 3 4 5 1
La unul din puncte mi se cere sa arat ca T*α =α*T stiind ca T apartine S5 si
T*α^2 =α^2*T. Cum fac asta? Am calculat cateva puteri ale lui α si am observat faptul ca α^5=e (permutare identica)


Plecand de la constatarea ta ca σ^5=e atunci σ^6=σ considerand pe T=σ^3 putem avea;
T. σ=σ^3.σ^6=σ.T=σ^6.σ^3 si la fel; T. σ^2=σ^3.σ^7=σ^2.T=σ^7.σ^3 DeciT=σ^3=(■(1 2 3 4 5@4 5 1 2 3))
OBS; Solutii pot fi ; T=σ^k, pentru k={1,2,3,4,5}
Deoarece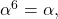 egalitatea cerută devine
egalitatea cerută devine 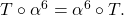
Vom arăta asta folosind ipoteza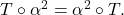
Astfel, avem