Buna ziua!Vineri am teza si am cate exercitii neclare.
1) |x| < 2
|y| < 2
Din alea 2 => |(2x+2y)/(4+xy)| < 1
Exercitiul asta l-am inceput in felul urmator dar m-am blocat.
-2<x<2
-2<y<2
Aratam ca -1<(2x+2y)/(4+xy)<1 /*(4+xy)
-4-xy<2x+2y<4+xy si de aici nu stiu ce sa fac.Nu inteleg ce trebuie sa facem in acest exercitiu.
2) [x]+[x+1]+[x+2]+…+[x+2015]=1+2+…+2015+2016
Asta l-am facut dar nu cred ca l-am rezolvat corect.Am procedat asa:
[x]+[x]+1+[x]+2+…+[x]+2015=1+2+…+2015+2016
Si aici e intrebarea mea: partile intregi se pot aduna ? De ex [x]+[x]=[2x] ?
Asa am procedat la exercitiul asta:
Daca am fi sa adunam partile intregi ale lui x ar fi [x]+[x]+…[x] de 2015 ori.
[2015x] = 2016 deoarece 1+2+…+2015 din dreapta se reduc cu ceilalti din stanga si in dreapta ramanand doar 2016.
Alta intrebare: Daca avem un asa exemplu avem voie sa impartim la 2015 ? Ca sa aflam doar [x] ? Eu asa am facut:
[2015x] = 2016 /: 2015 = > [x] = 1.0004 deci x = 1
3)ABCD paralelogram.Punctele M,N,P,Q astfel incat: CM=2MD , DN=2NB , CP=-1/3*BC , DQ = 2CQ ( toate segmentele sunt vectori )
a) Aratati ca triunghiurile MNP si BCD au acelasi centru de greutate ( asta l-am rezolvat )
b)Aratati ca oricare ar fi pct. O din planul paralelogramului poate avea loc relatia OA+OC=OB+OD ( la fel segmentele sunt vectori ) – aici nu stiu cum sa fac.Stiu ca , cu ajutorul acestei relatii demonstram ca un patrulater este paralelogram.
Multumesc


1. |x|<2 <==> -2<x<2 <==> x+2>0 si 2-x>0.
La fel si pentru y.
(x+2)(y+2)>0
(2-x)(2-y)>0.
Vezi ce poti obtine din cele 2 relatii.
Mai trebuie demonstrat ca 4+xy>0.
2.
Relatia [x]+[x]=[2x] nu este adevarata mereu. Contraexemplu pentru x=1.5.
Evident nu este cum ai zis tu.
[x]+..[x+2015]=1+..+2016
De la 0 la 2015 sunt 2016 termeni!!
[x]+..[x+2015]=1+..+2016 => 2016[x]=2016 => [x]=1=> x apartine [1,2).
Nu se poate sa nu-ti fi spus nimeni, sau sa nu fi aflat singur ca: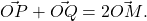
i) orice segment are un mijloc;
ii) Daca M este mijlocul segmentului [PQ], atunci oricare ar fi O: