Să se scrie ecuatia dreptei, dacă A(-2;3) se află pe o dreaptă perpendicular pe 2x-3y+8=0.
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Să se scrie ecuatia dreptei, dacă A(-2;3) se află pe o dreaptă perpendicular pe 2x-3y+8=0.
Salut,
Ecuaţia dreptei (d1): 2x-3y+8=0 se mai poate scrie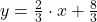
, deci m1 (panta dreptei d1) este 2/3.
Asta vine dintr-o altă formă a ecuaţiei dreptei: y=mx+n, unde m este panta dreptei, iar n este valoarea cu care dreapta se depărtează de axa Ox.
Dreapta d2 este perpendiculară pe dreapta d1 dacă m1 * m2 = -1, deci m2=-3/2.
Deci căutăm ecuaţia dreptei d2, care are panta -3/2 şi trece prin punctul A(-2,3).
Ecuaţia este y – yA = m2 * (x-xA), sau y – 3= -3/2 * (x+2), restul de rezolvat îţi las ţie.
Green eyes.