Salut,
Ma puteti ajuta cu o problema de statistica. Nu vreau rezultatul ci rationamentul. Multumesc.
Zece bile se repartizeaza la intamplare in 4 urne. Care este probabilitatea ca macar una sa fie goala?
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Problema nu e de statistică, e de probabilităti. Ideea e următoarea: fie a,b,c,d numerele bilelor repartizate în cele patru urne 1,2,3,4. Pentru a afla numărul cazurilor favorabile, trebuie determinat numărul de solutii în numere întregi nenegative ale ecuatiei diofantice liniare a+b+c+d=10. Acesta este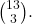
Vom calcula acum numărul cazurilor nefavorabile, adică acelea în care nici o urnă nu este goală. Acesta este egal cu numărul solutiilor aceleiasi ecuatii, dar în numere întregi strict pozitive. Acesta este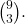
Prin urmare, probabilitatea căutată este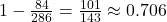
Salut Gigel,
Ai dreptate e o problema de probabilitati. Asta denota nivelul cunostintelor mele la aceasta materie.
Te rog mult sa-mi spui cum ai ajuns la rezultatele alea ca nu ma prind.
Eu am facut o functie C de numarare si am obtinut 270 de posibilitati in care a+b+c+d=10
Din acestea in 186 de cazuri a || b|| c || d = 0
Problema are inca 6 subpuncte, dar daca reusesc sa-l inteleg pe asta pe celelalte o sa pot singur.
Mersi.
In câte moduri se pot repartiza n bile în k urne?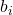 îi corespunde un număr de la 1 la k, numărul unicei urne
îi corespunde un număr de la 1 la k, numărul unicei urne 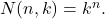
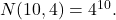
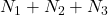 , adică numărul funcţiilor cu exact
, adică numărul funcţiilor cu exact 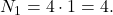
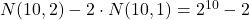 funcţii care iau ambele valori. Cele 2 urne pot fi alese
funcţii care iau ambele valori. Cele 2 urne pot fi alese  moduri, deci
moduri, deci 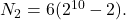
![Rendered by QuickLaTeX.com N_3=C_4^3[3^{10}-C_3^2(2^{10}-2)-C_3^1\cdot 1]=4(3^{10}-3\cdot 2^{10}+3).](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-67bc7157bf8d7e5f9ed80c7a15c959ff_l3.png)
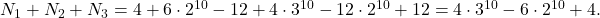
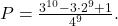
Dacă am realizat o astfel de repartizare, atunci fiecărei bile
în care a fost repartizată. Asta înseamnă că fiecărei repartizări îi corespunde o funcţie definită pe mulţimea {1, 2, …, n} cu
valori în mulţimea {1, 2, …, k}, iar la repartizări diferite corespund funcţii diferite. Numărul repartizărilor va fi egal cu cel al
funcţiilor respective, adică
Aşadar, numărul tuturor modurilor în care se pot repartiza 10 bile în 4 urne este
Numărătorul probabilităţii noastre va fi numărul funcţiilor nesurjective,
o valoare, 2 valori, sau 3 valori.
Dacă am ales valoarea (urna), există o singură funcţie constantă; cum sunt 4 urne, avem că
Dacă am ales 2 urne, există
în
Analog,
In final,
Multumesc mult ghioknt,
Nu-mi ramane dacat sa te cred pe cuvant. Foarte elaborata demonstratia ta dar ma depaseste. Nu inteleg de ce solutia data de Gigel n-ar fi buna chiar daca n-am inteles cum a ajuns la ea. Lasand matematica la o parte, chiar daca suntem pe un forum de matematica incearca sa-mi spui unde gresesc.
In continuare am numarat cazurile in care se pot aranja bilele:
Fiecare linie are suma bilelor din urne = 10
La fiecare linie care contine cel putin un 0 am adaugat „ZERO”
In final am obtinut 286 de cazuri posibile si 202 favorabile care acum imi dau seama ca este rezultatul pe care l-a dat Gigel.
202/286=0.706
1] 0+0+0+10 = 10 –> ZERO
2] 0+0+1+9 = 10 –> ZERO
3] 0+0+2+8 = 10 –> ZERO
4] 0+0+3+7 = 10 –> ZERO
5] 0+0+4+6 = 10 –> ZERO
6] 0+0+5+5 = 10 –> ZERO
7] 0+0+6+4 = 10 –> ZERO
8] 0+0+7+3 = 10 –> ZERO
9] 0+0+8+2 = 10 –> ZERO
10] 0+0+9+1 = 10 –> ZERO
11] 0+0+10+0 = 10 –> ZERO
12] 0+1+0+9 = 10 –> ZERO
13] 0+1+1+8 = 10 –> ZERO
14] 0+1+2+7 = 10 –> ZERO
15] 0+1+3+6 = 10 –> ZERO
16] 0+1+4+5 = 10 –> ZERO
17] 0+1+5+4 = 10 –> ZERO
18] 0+1+6+3 = 10 –> ZERO
19] 0+1+7+2 = 10 –> ZERO
20] 0+1+8+1 = 10 –> ZERO
21] 0+1+9+0 = 10 –> ZERO
22] 0+2+0+8 = 10 –> ZERO
23] 0+2+1+7 = 10 –> ZERO
24] 0+2+2+6 = 10 –> ZERO
25] 0+2+3+5 = 10 –> ZERO
26] 0+2+4+4 = 10 –> ZERO
27] 0+2+5+3 = 10 –> ZERO
28] 0+2+6+2 = 10 –> ZERO
29] 0+2+7+1 = 10 –> ZERO
30] 0+2+8+0 = 10 –> ZERO
31] 0+3+0+7 = 10 –> ZERO
32] 0+3+1+6 = 10 –> ZERO
33] 0+3+2+5 = 10 –> ZERO
34] 0+3+3+4 = 10 –> ZERO
35] 0+3+4+3 = 10 –> ZERO
36] 0+3+5+2 = 10 –> ZERO
37] 0+3+6+1 = 10 –> ZERO
38] 0+3+7+0 = 10 –> ZERO
39] 0+4+0+6 = 10 –> ZERO
40] 0+4+1+5 = 10 –> ZERO
41] 0+4+2+4 = 10 –> ZERO
42] 0+4+3+3 = 10 –> ZERO
43] 0+4+4+2 = 10 –> ZERO
44] 0+4+5+1 = 10 –> ZERO
45] 0+4+6+0 = 10 –> ZERO
46] 0+5+0+5 = 10 –> ZERO
47] 0+5+1+4 = 10 –> ZERO
48] 0+5+2+3 = 10 –> ZERO
49] 0+5+3+2 = 10 –> ZERO
50] 0+5+4+1 = 10 –> ZERO
51] 0+5+5+0 = 10 –> ZERO
52] 0+6+0+4 = 10 –> ZERO
53] 0+6+1+3 = 10 –> ZERO
54] 0+6+2+2 = 10 –> ZERO
55] 0+6+3+1 = 10 –> ZERO
56] 0+6+4+0 = 10 –> ZERO
57] 0+7+0+3 = 10 –> ZERO
58] 0+7+1+2 = 10 –> ZERO
59] 0+7+2+1 = 10 –> ZERO
60] 0+7+3+0 = 10 –> ZERO
61] 0+8+0+2 = 10 –> ZERO
62] 0+8+1+1 = 10 –> ZERO
63] 0+8+2+0 = 10 –> ZERO
64] 0+9+0+1 = 10 –> ZERO
65] 0+9+1+0 = 10 –> ZERO
66] 0+10+0+0 = 10 –> ZERO
67] 1+0+0+9 = 10 –> ZERO
68] 1+0+1+8 = 10 –> ZERO
69] 1+0+2+7 = 10 –> ZERO
70] 1+0+3+6 = 10 –> ZERO
71] 1+0+4+5 = 10 –> ZERO
72] 1+0+5+4 = 10 –> ZERO
73] 1+0+6+3 = 10 –> ZERO
74] 1+0+7+2 = 10 –> ZERO
75] 1+0+8+1 = 10 –> ZERO
76] 1+0+9+0 = 10 –> ZERO
77] 1+1+0+8 = 10 –> ZERO
78] 1+1+1+7 = 10
79] 1+1+2+6 = 10
80] 1+1+3+5 = 10
81] 1+1+4+4 = 10
82] 1+1+5+3 = 10
83] 1+1+6+2 = 10
84] 1+1+7+1 = 10
85] 1+1+8+0 = 10 –> ZERO
86] 1+2+0+7 = 10 –> ZERO
87] 1+2+1+6 = 10
88] 1+2+2+5 = 10
89] 1+2+3+4 = 10
90] 1+2+4+3 = 10
91] 1+2+5+2 = 10
92] 1+2+6+1 = 10
93] 1+2+7+0 = 10 –> ZERO
94] 1+3+0+6 = 10 –> ZERO
95] 1+3+1+5 = 10
96] 1+3+2+4 = 10
97] 1+3+3+3 = 10
98] 1+3+4+2 = 10
99] 1+3+5+1 = 10
100] 1+3+6+0 = 10 –> ZERO
101] 1+4+0+5 = 10 –> ZERO
102] 1+4+1+4 = 10
103] 1+4+2+3 = 10
104] 1+4+3+2 = 10
105] 1+4+4+1 = 10
106] 1+4+5+0 = 10 –> ZERO
107] 1+5+0+4 = 10 –> ZERO
108] 1+5+1+3 = 10
109] 1+5+2+2 = 10
110] 1+5+3+1 = 10
111] 1+5+4+0 = 10 –> ZERO
112] 1+6+0+3 = 10 –> ZERO
113] 1+6+1+2 = 10
114] 1+6+2+1 = 10
115] 1+6+3+0 = 10 –> ZERO
116] 1+7+0+2 = 10 –> ZERO
117] 1+7+1+1 = 10
118] 1+7+2+0 = 10 –> ZERO
119] 1+8+0+1 = 10 –> ZERO
120] 1+8+1+0 = 10 –> ZERO
121] 1+9+0+0 = 10 –> ZERO
122] 2+0+0+8 = 10 –> ZERO
123] 2+0+1+7 = 10 –> ZERO
124] 2+0+2+6 = 10 –> ZERO
125] 2+0+3+5 = 10 –> ZERO
126] 2+0+4+4 = 10 –> ZERO
127] 2+0+5+3 = 10 –> ZERO
128] 2+0+6+2 = 10 –> ZERO
129] 2+0+7+1 = 10 –> ZERO
130] 2+0+8+0 = 10 –> ZERO
131] 2+1+0+7 = 10 –> ZERO
132] 2+1+1+6 = 10
133] 2+1+2+5 = 10
134] 2+1+3+4 = 10
135] 2+1+4+3 = 10
136] 2+1+5+2 = 10
137] 2+1+6+1 = 10
138] 2+1+7+0 = 10 –> ZERO
139] 2+2+0+6 = 10 –> ZERO
140] 2+2+1+5 = 10
141] 2+2+2+4 = 10
142] 2+2+3+3 = 10
143] 2+2+4+2 = 10
144] 2+2+5+1 = 10
145] 2+2+6+0 = 10 –> ZERO
146] 2+3+0+5 = 10 –> ZERO
147] 2+3+1+4 = 10
148] 2+3+2+3 = 10
149] 2+3+3+2 = 10
150] 2+3+4+1 = 10
151] 2+3+5+0 = 10 –> ZERO
152] 2+4+0+4 = 10 –> ZERO
153] 2+4+1+3 = 10
154] 2+4+2+2 = 10
155] 2+4+3+1 = 10
156] 2+4+4+0 = 10 –> ZERO
157] 2+5+0+3 = 10 –> ZERO
158] 2+5+1+2 = 10
159] 2+5+2+1 = 10
160] 2+5+3+0 = 10 –> ZERO
161] 2+6+0+2 = 10 –> ZERO
162] 2+6+1+1 = 10
163] 2+6+2+0 = 10 –> ZERO
164] 2+7+0+1 = 10 –> ZERO
165] 2+7+1+0 = 10 –> ZERO
166] 2+8+0+0 = 10 –> ZERO
167] 3+0+0+7 = 10 –> ZERO
168] 3+0+1+6 = 10 –> ZERO
169] 3+0+2+5 = 10 –> ZERO
170] 3+0+3+4 = 10 –> ZERO
171] 3+0+4+3 = 10 –> ZERO
172] 3+0+5+2 = 10 –> ZERO
173] 3+0+6+1 = 10 –> ZERO
174] 3+0+7+0 = 10 –> ZERO
175] 3+1+0+6 = 10 –> ZERO
176] 3+1+1+5 = 10
177] 3+1+2+4 = 10
178] 3+1+3+3 = 10
179] 3+1+4+2 = 10
180] 3+1+5+1 = 10
181] 3+1+6+0 = 10 –> ZERO
182] 3+2+0+5 = 10 –> ZERO
183] 3+2+1+4 = 10
184] 3+2+2+3 = 10
185] 3+2+3+2 = 10
186] 3+2+4+1 = 10
187] 3+2+5+0 = 10 –> ZERO
188] 3+3+0+4 = 10 –> ZERO
189] 3+3+1+3 = 10
190] 3+3+2+2 = 10
191] 3+3+3+1 = 10
192] 3+3+4+0 = 10 –> ZERO
193] 3+4+0+3 = 10 –> ZERO
194] 3+4+1+2 = 10
195] 3+4+2+1 = 10
196] 3+4+3+0 = 10 –> ZERO
197] 3+5+0+2 = 10 –> ZERO
198] 3+5+1+1 = 10
199] 3+5+2+0 = 10 –> ZERO
200] 3+6+0+1 = 10 –> ZERO
201] 3+6+1+0 = 10 –> ZERO
202] 3+7+0+0 = 10 –> ZERO
203] 4+0+0+6 = 10 –> ZERO
204] 4+0+1+5 = 10 –> ZERO
205] 4+0+2+4 = 10 –> ZERO
206] 4+0+3+3 = 10 –> ZERO
207] 4+0+4+2 = 10 –> ZERO
208] 4+0+5+1 = 10 –> ZERO
209] 4+0+6+0 = 10 –> ZERO
210] 4+1+0+5 = 10 –> ZERO
211] 4+1+1+4 = 10
212] 4+1+2+3 = 10
213] 4+1+3+2 = 10
214] 4+1+4+1 = 10
215] 4+1+5+0 = 10 –> ZERO
216] 4+2+0+4 = 10 –> ZERO
217] 4+2+1+3 = 10
218] 4+2+2+2 = 10
219] 4+2+3+1 = 10
220] 4+2+4+0 = 10 –> ZERO
221] 4+3+0+3 = 10 –> ZERO
222] 4+3+1+2 = 10
223] 4+3+2+1 = 10
224] 4+3+3+0 = 10 –> ZERO
225] 4+4+0+2 = 10 –> ZERO
226] 4+4+1+1 = 10
227] 4+4+2+0 = 10 –> ZERO
228] 4+5+0+1 = 10 –> ZERO
229] 4+5+1+0 = 10 –> ZERO
230] 4+6+0+0 = 10 –> ZERO
231] 5+0+0+5 = 10 –> ZERO
232] 5+0+1+4 = 10 –> ZERO
233] 5+0+2+3 = 10 –> ZERO
234] 5+0+3+2 = 10 –> ZERO
235] 5+0+4+1 = 10 –> ZERO
236] 5+0+5+0 = 10 –> ZERO
237] 5+1+0+4 = 10 –> ZERO
238] 5+1+1+3 = 10
239] 5+1+2+2 = 10
240] 5+1+3+1 = 10
241] 5+1+4+0 = 10 –> ZERO
242] 5+2+0+3 = 10 –> ZERO
243] 5+2+1+2 = 10
244] 5+2+2+1 = 10
245] 5+2+3+0 = 10 –> ZERO
246] 5+3+0+2 = 10 –> ZERO
247] 5+3+1+1 = 10
248] 5+3+2+0 = 10 –> ZERO
249] 5+4+0+1 = 10 –> ZERO
250] 5+4+1+0 = 10 –> ZERO
251] 5+5+0+0 = 10 –> ZERO
252] 6+0+0+4 = 10 –> ZERO
253] 6+0+1+3 = 10 –> ZERO
254] 6+0+2+2 = 10 –> ZERO
255] 6+0+3+1 = 10 –> ZERO
256] 6+0+4+0 = 10 –> ZERO
257] 6+1+0+3 = 10 –> ZERO
258] 6+1+1+2 = 10
259] 6+1+2+1 = 10
260] 6+1+3+0 = 10 –> ZERO
261] 6+2+0+2 = 10 –> ZERO
262] 6+2+1+1 = 10
263] 6+2+2+0 = 10 –> ZERO
264] 6+3+0+1 = 10 –> ZERO
265] 6+3+1+0 = 10 –> ZERO
266] 6+4+0+0 = 10 –> ZERO
267] 7+0+0+3 = 10 –> ZERO
268] 7+0+1+2 = 10 –> ZERO
269] 7+0+2+1 = 10 –> ZERO
270] 7+0+3+0 = 10 –> ZERO
271] 7+1+0+2 = 10 –> ZERO
272] 7+1+1+1 = 10
273] 7+1+2+0 = 10 –> ZERO
274] 7+2+0+1 = 10 –> ZERO
275] 7+2+1+0 = 10 –> ZERO
276] 7+3+0+0 = 10 –> ZERO
277] 8+0+0+2 = 10 –> ZERO
278] 8+0+1+1 = 10 –> ZERO
279] 8+0+2+0 = 10 –> ZERO
280] 8+1+0+1 = 10 –> ZERO
281] 8+1+1+0 = 10 –> ZERO
282] 8+2+0+0 = 10 –> ZERO
283] 9+0+0+1 = 10 –> ZERO
284] 9+0+1+0 = 10 –> ZERO
285] 9+1+0+0 = 10 –> ZERO
286] 10+0+0+0 = 10 –> ZERO
286 – 202 = 0
Nu trebuie să mă crezi pe cuvânt. Nu sunt stăpânul adevărului! Diferenţa dintre soluţia mea şi cea a lui gigelmarga
rezultă din modul diferit în care interpretăm zisele tale: Zece bile se repartizeaza la intamplare in 4 urne.
Imaginează-ţi că se face un experiment de repartizare a celor 10 bile, în urma căruia urnele au conţinuturile:
{1,2,3}, {4,5,6}, {7,8,9}, {10}.
Apoi se repeta experienţa şi rezultă conţinuturile: {1,2,4}, {3,5,6}, {7,8,9}, {10}.
Eu am considerat că aceste rezultate reprezintă repartizări distincte, iar din punct de vedere probabilistic, ele
reprezintă evenimente elementare egal probabile.
Din punctul tău de vedere, ele nu sunt repartizări distincte, ci ele ilustrează o singură repartizare: 191] 3+3+3+1.
In acest caz, raţionamentul tău este corect, el nu face decât să arate că puteai să ai încredere în rezultatele lui gigelmarga.
O singură nedumerire am: cum descrii experienţa prin care repartiţia 1] şi repartiţia 191] din lista ta sunt egal probabile.
Eu zic că este ca şi cum ai spune: la aruncarea a 2 zaruri sunt posibile 11 sume; deci probabilitatea ca suma să fie 7
este 1/11.
Daca eram convins ca solutia data de Gigel e ok nu as mai fi intrebat. Pur si simplu mi-am dat seama ca rezultatul meu il avea si el. De asemenea nici nu mi-am dat seama ca exista loc de intrepretare. Eu am ales solutia cea mai simpla dar problema e ca nu am inteles de unde scoate gigelmarga rezultatele alea. Nu stiu ce inseamna (13 3) (9 3), de unde rezulta 84/286?
Vreau sa spun ca dupa „o anumita logica” am gasit solutia dar cum fac asta matematic vorbind. Caci la examen n-am calculator care sa-mi numere solutiile.
Multumesc pt. timpul acordat.
Acum incepe sa aiba sens. Mai ramane sa-mi explicati de ce a+b+c+d=10 are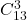 solutii si de ce numarul cazurilor nefavorabile este
solutii si de ce numarul cazurilor nefavorabile este 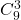 , si apoi dau o bere (doar la cei ce au trecut
, si apoi dau o bere (doar la cei ce au trecut  ani)
ani)
Multumesc.
Fie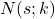 numărul soluţiilor în numere naturale ale ecuaţiei
numărul soluţiilor în numere naturale ale ecuaţiei 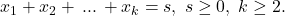
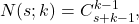 care apoi se poate demonstra, eventual prin inducţie.
care apoi se poate demonstra, eventual prin inducţie.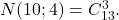
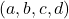 este o soluţie în numere naturale nenule a ecuaţiei
este o soluţie în numere naturale nenule a ecuaţiei 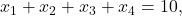
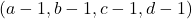 este o soluţie în numere naturale a ecuaţiei
este o soluţie în numere naturale a ecuaţiei 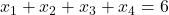 ,
, 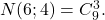
Empiric, se poate propune formula
Pentru s=10 şi k=4 se obtine
Observi apoi că dacă
atunci
corespondenţa între mulţimile soluţiilor fiind bijectivă. Aşadar, numărul soluţiilor primei ecuaţii este
Se pare că nu te-a preocupat deloc întrebarea mea: Cum descrii procedeul prin care zece bile se repartizează la întâmplare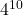 .
.
în 4 urne. în urma căruia repartiţiile din lista ta sunt egal probabile?
Pentru acelaşi text eu imaginez următoarea experienţă. Intr-o incintă ca cea de la extragerile loto, dar cu 4 ieşiri, se introduce
pe rând, câte o bilă pe care destinul o va împinge către una din cele 4 urne.
Sau: într-un bol am 4 bile, corespondentele celor 4 urne. In mâna stângă iau bila cu numărul 1, iar cu dreapta extrag
o bila din bol. Dacă pe ea scrie 2, bila numărul 1 merge în urna 2, iar bila din mâna dreaptă, înapoi iî bol şamd.
Cele 2 repartizări cu care am exemplificat in postul precedent se pot reprezenta sub forma (1,1,1,2,2,2,3,3,3,4), respectiv,
(1,1,2,1,2,2,3,3,3,4), adică prin tabele de valori ale unor funcţii ce pot lua 4 valori. Asta demonstrează că numărul tuturor
rezultatelor echiprobabile ale unei asemenea experienţe este
Să numărăm direct soluţiile ecuaţiei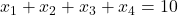 , adică să stabilim că
, adică să stabilim că 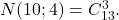
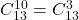 pentru că orice drum presupune parcurgerea a 13 stadii dintre
pentru că orice drum presupune parcurgerea a 13 stadii dintre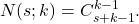
Să considerăm un sistem de axe, punctul S(3,10) şi un caroiaj format din ”străzile” x=0, x=1, x=2, x=3 şi aleile
y=0, y=1, y=2, …, y=10. Asociem fiecărei soluţii un ”drum” care leagă punctul O de punctul S, ca în exemplul următor.
Pentru soluţia (0,5,2,3) asociez ruta: pe prima ”stradă” nu merg deloc, ci mă deplasez pe ”aleea” y=0 până în punctul A(1,0);
pe a doua ”stradă” parcurg 5 stadii, până în B(1,5), apoi la dreapta pe ”alee” până în C(2,5); pe a treia ”stradă” merg 2
stadii, până în D(2,7), iarăşi la dreapta până în E(3,7), în final, pe a patra ”stradă” ultimele 3 stadii, până în S.
Sper că ai înţeles principiul; important este că se stabileşte o corespondenţă bijectiva între mulţimea soluţiilor şi mulţimea
drumurilor O – S. Deci în loc să numărăm soluţiile, numărăm drumurile, ceeace este mai simplu.
Numărul drumurilr este
care trebuie să alegem o submulţime de 10 pe care să le parcurgem pe ,,străzi”, iar restul de 3, pe ”alei”.
Cu acelaşi procedeu se obţine şi rezultatul
Nu este vorba ca nu m-a preocupat intrebarea ta. Dar dupa logica mea fiecare din evenimentele ce am enumerat sunt egal probabile, pt ca bilele nu sunt numerotate deci nu se pot deosebi.
Daca exista loc de interpretare atunci am preferat varianta mai simpla si dupa ce o sa o inteleg complet o sa reiau si celalalt caz.
Am inteles exemplul cu drumurile dar mai am o nedumerire. Daca strada x0 este axa OY atunci aleea y0 ar trebui sa fie axa OX. In acest caz rezulta ca am 11 alei. Gresesc?
Deci numarul solutiilor o sa fie N(14,10)?
In postul anterior spuneai ca daca (a-1,b-1,c-1,d-1) atunci x1+x2+x3+x4=6. De ce ai scazut 1? De ce nu 2, 3, etc?
Iti multumesc pt. ca azi am mai invatat de la tine ca
Cele 10 bile sunt obiecte concrete, distincte. Dacă urna 1 va avea în final o singură bilă, atunci în ea nu se va afla noţiunea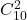 moduri, iar distribuţia 1+2+4+3 se poate realiza în
moduri, iar distribuţia 1+2+4+3 se poate realiza în
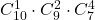 moduri. Este o greşeală să nu îţi imaginezi că bilele sunt numerotate, chiar
moduri. Este o greşeală să nu îţi imaginezi că bilele sunt numerotate, chiar 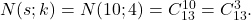 N(14;10) este o aberaţie, de unde ai scos-o?
N(14;10) este o aberaţie, de unde ai scos-o?
”o bilă”, ci o bilă concretă dintre cele 10. Evenimentul U_1 conţine o bilă se poate realiza în 10 moduri, evenimentul U_2
conţine 2 bile se realizează în
dacă, concret, ele sunt otova.
Sunt 4 drumuri care corespund celor 4 necunoscute din ecuaţie şi 11 alei între care se află 10 spaţii (stadii, cum
le-am numit eu) pe verticală corespunzătoare totalului de 10 pe care să mi-l furnizeze cele 4 drumuri.
Intre cele 4 drumuri există 3 stadii orizontale, a. î. orice drum de la O la S este format din 13 stadii, dintre care 10 sunt verticale.
Deaceea
O soluţie de numere naturale nenule conţine numere de la 1 în sus, nu de la 2 sau 3 în sus, cum sugerezi tu.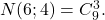
Astfel soluţia de numere naturale nenule (2,1,4,3), cu s=10, se trasformă în soluţia (1,0,3,2), de numere naturale,
inclusiv 0 a ecuaţiei cu s=6, iar despre numărul acestor soluţii ştim că este
Problemă:
Care este numărul soluţiilor ecuaţiei diofantice
Aceasta problemă se rezolva prin inducţie matematică şi anume:
1)- Pentru
2)- Pentru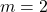 , ecuaţia diofantică
, ecuaţia diofantică 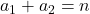 are
are
soluţii de forma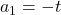 şi
şi 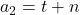 unde
unde 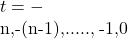 iar numărul soluţiilor este
iar numărul soluţiilor este 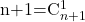
3)- Pentru ecuaţia diofantică
ecuaţia diofantică 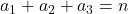 se
se
mai scrie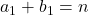 care are soluţii de
care are soluţii de
forma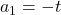 şi
şi 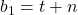 unde
unde 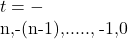 şi se observă uşor că numărul soluţiilor este
şi se observă uşor că numărul soluţiilor este
––––
4)- Pentru cazul general numărul soluţiilor este
numărul soluţiilor este
Se arată uşor ca numărul soluţiilor pentru cazul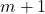 este cel de mai sus dacă se înlocuieşte
este cel de mai sus dacă se înlocuieşte  cu
cu 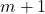 .
.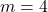 şi
şi 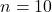 obţinem ca număr de soluţii valoarea
obţinem ca număr de soluţii valoarea 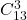 .
.
Particularizând rezultă imediat că pentru
Cum calculăm numărul soluţiilor ecuaţiei diofantice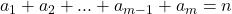 ştiind că
ştiind că 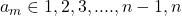 iar
iar  este un număr natural bine stabilit astfel încât
este un număr natural bine stabilit astfel încât  ?
?
Cum , notam
, notam 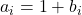 cu
cu 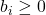
Astfel ecuatia devine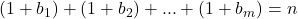 sau
sau 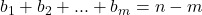
Astfel am ajuns in situatia deja studiata. Trebuie sa determinam numerele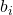 , care de-acum pot lua inclusiv valoarea 0, doar ca suma lor de data asta nu este n, ci n-m. Numarul solutiilor e data de formula anterioara, doar ca in loc de n trebuie pus n-m.
, care de-acum pot lua inclusiv valoarea 0, doar ca suma lor de data asta nu este n, ci n-m. Numarul solutiilor e data de formula anterioara, doar ca in loc de n trebuie pus n-m.
Corect!