Fie trapezul ABCD inscris in cercul de centru O si raza r , AB || BC , AB>CD .
AB = 2AD = 12 cm si BD = 6√3 cm .
Aflati raza si aria triunghiului OBD .
AniDeȘcoală.ro Latest Intrebari
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Fie trapezul ABCD inscris in cercul de centru O si raza r , AB || BC , AB>CD .
AB = 2AD = 12 cm si BD = 6√3 cm .
Aflati raza si aria triunghiului OBD .
Buna seara
Mai verificati odata va rog textul problemei:AB nu poate fi cred paralela cu BC.Doua drepte care au un punct comun nu pot fi paralele decat daca se suprapun.
Buna seara
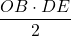Inaltimea triunghiului BOD este egala cu DE care se determina scriind suprafata triunghiului ADB in doua feluri egale si anume:
De aici rezulta 
iar suprafata triunghiului BOD este egala cu
Cred ca figura este cea reprezentata de mine mai jos.
Din triunghiul ADB observam ca
Triunghiul ABD este deci dreptunghic deoarece respecta teorema lui Pitagora si se inscrie intr-un semicerc avand deci AB=2r cu raza r=6 cm.
Suprafata triunghiului BOD este egala cu
Multumesc . Si da , era AB || CD .