Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Fie ABC un triunghi isoscel cu AB=AC. Fie D apartinand BC si E apartinand (AC) astfel incat AD perpendicular pe BC si DE perpendicular pe AC. Notam cu F mijlocul lui DE. Se se arate ce AF perpendicular pe BE.
M-am gandit ca trebuie demonstrat ca AF produs scalar cu BE este egal cu 0. AF este mediana in tr ADE deci AF=1/2(AD+AE) (scrisi ca vectori)
AD este mediana in tr ABC deci AD=1/(AB+AC).
Orice ajutor este binevenit. Multumesc anticipat.
[/code]
Te rog sa faci un desen conf.problemei.Mai du segmentele;BG_l_AC , CI_l_AB, ,EJ_l_AB , DL_l_AB , LM_l_ACTinand seama de simetria triunghiului isoscel fata de inaltimea AD,vom nota cu H=intersectia lui AD cu CI si BG , cu K=intersectia lui AD cu EJ si LM , cu S=intersectia lui BG cu EJ , cu T=intersectia luiCI cu LM ,
cu R=intersectia luiCI cu DE si cu Q=intersectia luiBG cu DL. In triungiurile;CBG si CIB, seg. DE siDL sunt linii mijlocii si vom avea ; CR=RH=ES=BQ=QH= LT=DR=DQ=b .La fel , in triunghiurile ;CHG si BHI seg.ES si LT sunt linii mijlocii si vom avea; RE=HS=SG=TK=HT=TI=HQ=SK=a.Cum BG_l_AE si EJ_l_AB, S va fi ortocentrul triunghiuluiAEB ,deci AS este _l_EB. Dar AS este mediana in triunghiulAGH si cumDE//BG , AS in prelungire , va fi mediana si in triunghiulAED si cum F este mijlocul lui DE,rezulta ca AF_l_EB
Pentru o soluţie care foloseşte produsul scalar, scrie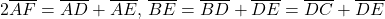
şi apoi asemănarea triunghiurilor ADE şi DCE, de unde va rezulta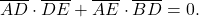 
Domnule ”gigelmarga”,apreciez cu toata fiinta mea si va multumesc din toata inima pentru modul in care ma ”tratati”.Sunteti un educator demn de toata admiratia. Va stimez foarte mult.Dumnezeu sa va binecuvinteze
Cat priveste problema,mie imi place foarte mult geometria sintetica si problema mi s-a parut chiar draguta si am tratat-o ca atare.Va multumesc pentru solutia vectoriala. Cu deosebit respect.DD
@DD Nu vă „tratez” nicicum. Titlul acestui fir de discuţii făcea referire la produsul scalar şi m-am gândit că o indicaţie în acest sens ar fi utilă.
Şi mie îmi place geometria sintetică. Iată o soluţie alternativă:
Luăm M mijlocul segmentului CE. Atunci MF e paralel cu CD, deci perpendicular pe AD. Totodată, DF e perpendicular pe AC. Deducem că F este ortocentrul triunghiului ADM, aşadar AF e perpendicular pe MD, care, fiind linie mijlocie în triunghiul BCE, este paralel cu BE.