Am de demonstrat urmatoarea inegalitate folosind inductia matematica:
n! mai mare 2^n oricare ar fi n natural mai mare sau egal cu 4.
La pasul 1 am verificat daca p(4) este adevarat. Apoi, la pasul 2 am presupus ca p(k) adevarat adica k! mai mare 2^k. Apoi trebuie demonstrat ca p(k+1) adevarat adica (k+1)! mai mare 2^(k+1). Cum rezolv in continuare? As prefera ca raspunsul sa fie cat mai explicit. Multumesc anticipat.


Pasul doi este urmatorul: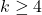 si
si 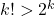 . Atunci
. Atunci 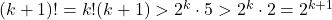 .
.
Fie
Va multumesc pentru raspuns dar imi puteti explica , va rog, de unde deducem ca (k+1)!=k!(k+1)? Exista vreo formula speciala?
Factorialul este o functie pe multimea numerelor naturale cu valori pe aceeasi multime. Dar este o functie definita prin recursie.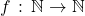 se numeste factorial daca:
se numeste factorial daca:
 ;
;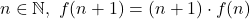 .
.
Definitie: Functia
Pentru orice
Deci pentru orice numar intreg pozitiv , avem
, avem 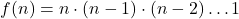 , iar
, iar  . Acest numar (
. Acest numar (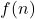 ,
,  ) se numeste
) se numeste  factorial, care se noteaza asa:
factorial, care se noteaza asa: 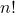 .
.
Asadar raspunsul la intrebare este: „Prin definitie”.
Acum am inteles. Multumesc.