Un coleg de pe forum mi-a aratat aceasta problema si sunt curios cu ce alte abordari ati putea veni
Care este valoarea lui L ?
![Rendered by QuickLaTeX.com \[ L = \lim _{n \to \infty } \sum\limits_{k = 1}^n {\ln (1 + \frac{k}{{n^2 }}} ) \]](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-29b2fac6b9dbc8574a5bb7b51b8978c6_l3.png)
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Pntru inceput ,expresia ”lim(n->inf)[ln(1+k/n^2)]” o vom pune sub forma;
”lim(n->inf.)[(1/n).(n,ln(1+k/n^2))]=lim(n->inf.)[(1/n).ln{lim(n->inf.)[(1+(k/n)/n)^n)]}=lim(n->inf.)[(1/n)ln(e^k/n)]=lim(n->inf.)[(1/n).(k/n)]”
lim(n->inf.)[Suma(de la k=1 la n)[ln(1+k/n^2)]=lim(n->inf.)[suma( de la k=1 la n)[k/n^2]=lim(n->inf.)[n(n+1)/(2n^2)]->1/2
Avem urmatoarea limita remarcabila
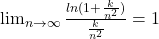 .Care in limbaj cu epsilon devine,
.Care in limbaj cu epsilon devine,![Rendered by QuickLaTeX.com |\frac{ln(1+\frac{k}{n^2})}{\frac{k}{n^2}}-1|<\epsilon\Leftrightarrow -\epsilon<\frac{ln(1+\frac{k}{n^2})}{\frac{k}{n^2}}-1<\epsilon \Leftrightarrow 1-\epsilon<\frac{ln(1+\frac{k}{n^2})}{\frac{k}{n^2}}<\epsilon+1 \Leftrightarrow (1-\epsilon) \cdot \frac{k}{n^2}<ln(1+\frac{k}{n^2})<(1+\epsilon) \cdot \frac{k}{n^2} \Leftrightarrow (1-\epsilon)\cdot \sum\limits_{k=1}^n \frac{k}{n^2}<\sum\limits_{k=1}^n ln(1+\frac{k}{n^2})<(1+\epsilon)\cdot \sum\limits_{k=1}^n \frac{k}{n^2} \Leftrightarrow 1-\epsilon<\frac{\sum\limits_{k=1}^n ln(1+\frac{k}{n^2})}{\sum\limits_{k=1}^n \frac{k}{n^2}}<1+\epsilon \Leftrightarrow |\frac{\sum\limits_{k=1}^n ln(1+\frac{k}{n^2})}{\sum\limits_{k=1}^n \frac{k}{n^2}}-1|<\epsilon \Leftrightarrow \lim _{n \to \infty }\frac{\sum\limits_{k=1}^n ln(1+\frac{k}{n^2})}{\sum\limits_{k=1}^n \frac{k}{n^2}}=1[tex],dar \lim _{n \to \infty } \sum\limits_{k=1}^n \frac{k}{n^2}=\frac{1}{2}](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-c8dc47b1a365eac96bbec2e9647de509_l3.png) .Deducem ca si limta ceruta este
.Deducem ca si limta ceruta este  .
.
@ grapefruit
Pentru ca stiu ca observatiile mele nu te vor supara, imi permit sa fiu critic cu cele postate de tine.
Mai intai, aceasta abordare superficiala a problemei nu poate fi justificata cu expresia ”limbajul cu epsilon”.
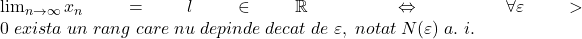
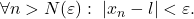
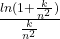 , deduci ca pentru fiecare
, deduci ca pentru fiecare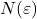 dincolo de care sunt adevarate inegalitatile scrise de tine, dar, pe ansamblu, acestia
dincolo de care sunt adevarate inegalitatile scrise de tine, dar, pe ansamblu, acestia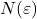
Teorema cu pricina se numeste deobicei ”Teorema de caracterizare cu epsilon a limitei unui sir”, sau, alteori,
”Definitia cu epsilon a limitei unui sir”. Este vorba de siruri convergente si are urmatorul enunt:
Cand aplici aceasta teorema sirurilor de forma
exista un
vor fi diferiti de la sir la sir, deci vor depinde, vrei, nu vrei si de k, nu numai de epsilon.
Atunci cand vrei sa demonstrezi ca raportul celor 2 sume are limita 1, accentul trebuie pus pe evidentierea unui
care sa nu depinda si de k; asta inseamna ca, ori nu este niciunul dintre cei gasiti anterior, ori este unul dintre ei, dar
trebuie precizat care anume. Ori tu nu sufli un cuvintel despre asta, probabil pe principiul: o problema despre care nu vorbim,
inseamna ca nu exista!
Iata, acum, o posibila demonstratie.
Am definit astfel pe
Dar
in cosecinta, inegalitatile
daca
trase de tine sunt acum justificate.
In speranta ca nu te-am bulversat prea tare,
cu bine,
ghioknt