Pentru t apartine R se defineste ![]()
Daca G={f_t |t apartine R},atunci (G,o) este grup abelian si (G,o) izomorf cu (R,+).
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Observaţie: dacă (demonstraţie banală)
(demonstraţie banală) compunerea funcţiilor este lege de compoziţie şi
compunerea funcţiilor este lege de compoziţie şi  este monoid.
este monoid. în raport cu compunerea funcţiilor, adică
în raport cu compunerea funcţiilor, adică 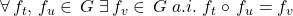 .
.
 .
. .
. , deci
, deci  este elementul neutru şi pe G.
este elementul neutru şi pe G. , ceeace arată că toate funcţiile din G sunt inversabile şi au inversele tot în G.
, ceeace arată că toate funcţiile din G sunt inversabile şi au inversele tot în G. este subgrup al monoidului
este subgrup al monoidului  , adică este grup.
, adică este grup.
 (cf. observaţiei iniţiale), deci legea de compoziţie indusă pe G este comutativă (G este subgrup comutativ al unui monoid necomutativ).
(cf. observaţiei iniţiale), deci legea de compoziţie indusă pe G este comutativă (G este subgrup comutativ al unui monoid necomutativ). este surjectivă pentru că orice funcţie din G este asociată unui număr real. Observaţia iniţială se poate scrie acum
este surjectivă pentru că orice funcţie din G este asociată unui număr real. Observaţia iniţială se poate scrie acum 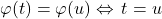 , deci este şi injectivă.
, deci este şi injectivă.
 , deci funcţia noastră este şi morfism.
, deci funcţia noastră este şi morfism.
0) Există o lege de compoziţie pe G?
Ştim că pe mulţimea
Să arătăm că G este parte stabilă a lui
Intr-adevăr,
Răspunsul la întrebare este: legea de compoziţie pe G este legea de compoziţie indusă pe G de compunerea funcţiilor pe
1)
2) Fie
Din 0), 1) si 2) deducem că
3) Evident funcţia
În concluzie grupurile (G, o) si (R, +) sunt izomorfe.
Cu bine, ghioknt.