Problema asta mi-a fost data la capitolul cu Sisteme Cramer. Deocamdata nu pot sa gasesc o legatura, dar orice rezolvare m-ar ajuta enorm.
Fie a,b,c numere reale strict pozitive, diferite de 1 si x, y, z numere reale astfel incat
![]() ;
;
![]() ;
;
![]() .
.
Sa se arate ca xyz-x-y-z=2.


Logaritmezi egalităţile şi obţii:
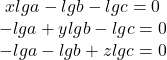
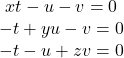 are soluţia nenulă (loga, logb, logc).
are soluţia nenulă (loga, logb, logc).
ceeace arată că sistemul omogen
Asta înseamnă că determinantul sistemului este nul, de unde obţii relaţia cerută.
Cu bine, ghioknt.