Aratati ca sirul (xn) cu xn=n/2n+1 nu converge la 2.
Si inca o intrebare, cum construiesc un sir cu o anumita limita? De exemplu, un sir cu limita 1 si nemonoton?
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Aratati ca sirul (xn) cu xn=n/2n+1 nu converge la 2.
Si inca o intrebare, cum construiesc un sir cu o anumita limita? De exemplu, un sir cu limita 1 si nemonoton?
Vom demonstra acest lucru ,prin reducere la absurd ,f olosind definitia cu e(epsilon) a convegentei . e apartine (0,1)
Presupunem ca sirul Xn –>2.Asadar conf definiytiei cu e putem spune ca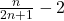
l=calcule=|
|= 
=
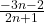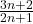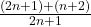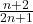=1+
>1
lxn-2l<e e apartine (o ,1)
Darl lxn-2l=l
Dar noi am presupus ca numarul din interiorul modulului este ,e<1
Asadar ipoteza ca 2 este limita sirului este falsa
Pt determinarea adevaratei limite a sirului vei face raportul coeficientilor lui n , atat de la numarator cat si de la numitor.
Adica lim Xn=1/2 cand n–>+oo
La pct b) exemplu
Xn=1+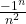
Xn este un sir nemonoton care tinde la 1
e