Home/ Intrebari/Q 83383
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

classius
Pe: 2013-10-14T15:41:42+03:00 In: In:

Limita

Sa se arate ca sirul are limita infinita:

a_{n}=n-n^{2}

Multumesc!

Similare

7 raspunsuri

  1. PallMall

        \[ \begin{array}{l} a_n = n - n^2 \\ {\lim }\limits_{n \to \infty } [n^2 (\frac{1}{n} - 1)] = - \infty \\ \end{array} \]

    de obicei cand ai limite in care n,x tind la infinit se da factor comun termenul cu exponentul mai mare(in cazul nostru n^2) si apoi o sa ai 1 supra n la o putere care va fi 0(zero) si tot asa totul de inmultit cu infinit ..si o sa iti dea + sau minus infinit.
    Poti sa aplici asta si in cazul raporturilor cand ai nedefinirea infinit supra infinit

  2. classius

    Nu am intrat inca asa de adanc in conceptul de limita, dar nu mi se atat de corect sa trantesc din prima o afirmatie de genul celei de mai sus pentru a demonstra ceva, as dori ceva mai elaborat…

  4. PallMall

        \[ \begin{array}{l} {\lim }\limits_{n \to \infty } \frac{1}{n} = 0 \\ {\lim }\limits_{n \to \infty } a = a \\ {\lim }\limits_{n \to \infty } n = \infty \\ si\,\,atunci\,\,avem \\ {\lim }\limits_{n \to \infty } (n - n^2 ) = {\lim }\limits_{n \to \infty } n^2 (\frac{1}{n} - 1) = {\lim }\limits_{n \to \infty } n^2 *\left( { {\lim }\limits_{n \to \infty } \frac{1}{n} - {\lim }\limits_{n \to \infty } ( - 1)} \right) = \infty *(0 - 1) = - \infty \\ \end{array} \]

    daca vrei mai elaborat ..uite asa
    sa imi zici daca ai inteles…

  5. xor_NTG
    maestru (V)

    Nu cred ca e ok sa intervin dar afirmatia domnului classius pare ilogica. Cum vreti ceva mai elaborat daca nu ati intrat asa de adanc in conceptul de limita? Exercitiul propus se rezolva utilizand reguli de calcul elementare pe dreapta reala incheiata respectiv cu aplicarea celei mai simple metode de calcul a unei limite: metoda factorului fortat.

    Domnul PallMall a prezentat modul de calcul (practic) a acestor tipuri de limite, ceea ce nu se gaseste in majoritatea manualelor.

    Sa fie doar o interpretare gresita?

  6. classius

    Am cerut asta deoarece in manualul meu de matematica, inainte de exercitiul asta este unul rezolvat, asemanator in care se cere sa se arate ca limita sirului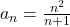 a_{n}=\frac{n^{2}}{n+1} este infinita.

    Aceasta demonstratie este facuta cu vecinatati, dar destul de slab incat sa imi lase niste semne de intrebare…

    Este vina mea deoarece nu am specificat o metoda de calcul.

  8. PallMall

    ti-as explica cu vecinatatile , dar sincer nu stiu cum sa iti arat ,deoarece este metoda mai mult grafica, pe o dreapta , nu am cum sa iti scriu aici , cel putin nu dispun de programele specifice.

  9. ghioknt
    profesor

    Am inţeles din postările precedente că problema trebuia formulată de classius astfel: să se arate, folosind definiţia cu vecinătăţi,
    că limita şirului cu pricina este infinită.
    Hiba la această definiţie este că cu ea nu poţi afla limita. Cu ea poţi să faci una din doua: ori să arăţi că un anumit l din
    Rbarat (pe care ţi-l dă cineva) este limita şirului, ori să arăţi că un anume element h al lui Rbarat nu este limita şirului.
    În primul caz ai de arătat că în orice vecinătate V a lui l se află toţi termenii şirului, începând de la un rang k (ce depinde de vecinătate);
    eu prefer să arăt că în afara oricărei vecinătăţi rămân un număr finit de termeni.
    În al doilea caz ai de arătat că există o vecinătate V a lui h care conţine doar un număr finit de termeni ai şirului, sau niciunul;
    eu prefer să arăt că exista V în afara căreia se află o infinitate de termeni.
    Enunţul arată ca am de ales între +oo si -oo. Să presupunem că sunt atât de năuc, încât mi se pare că limita ar fi +oo.
    Vecinătate oarecare a lui +oo înseamnă V=(a; oo), cu a>0 arbitrar. Câţi termeni rămân în afara lui V?

        \[ a_n \notin V \Leftrightarrow n - n^2 \le a \Leftrightarrow n^2 - n + a \ge 0 \Leftrightarrow n\,\,este\,\,o\,\,solutie\,\,naturala\,\,a\,\,inecuatiei\,\,x^2 - x + a \ge 0,\, \]

    care (pentru a=1 de exemplu)
    are soluţia R, deci orice n natural o satisface; altfel spus , toţi termenii şirului sunt în afara vecinătăţii (1; oo) a lui +oo,
    deci nu acesta este limita şirului.
    Vecinătate oarecare a lui -oo înseamnă V=(-oo; -a) cu a>0 arbitrar. Cîţi termeni rămân în afara lui V?

        \[ a_n \notin V \Leftrightarrow n - n^2 \ge - a \Leftrightarrow n^2 - n - a \le 0 \Leftrightarrow n\,\,este\,\,o\,\,solutie\,\,naturala\,\,a\,\,inecuatiei\,\,x^2 - x - a \le 0, \]

    care are soluţie de tipul
    [x1; x2] în care intră un număr finit de numere naturale, adică în afara oricărei vecinataţi a lui -oo se află un numar finit
    de termeni ai şirului, deci limita sa este -oo.
    A fost greu? Dacă te pregăteşti pentru facultatea de matematică, asemenea exerciţii, care vizează înţelegerea definiţiilor,
    sunt utile, dacă nu,probabilitatea să mai întâlneşti aşa ceva tinde la 0.
    Cu bine, ghioknt.

Raspunde

Raspunde