Se considera functiile f,g:R->R, f(x)=x^2 – x/2 – 3, g(x)=m, m este un numar real. Sa se determine in functie de m numarul de puncte de intersectie ale graficelor celor 2 functii.
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Se considera functiile f,g:R->R, f(x)=x^2 – x/2 – 3, g(x)=m, m este un numar real. Sa se determine in functie de m numarul de puncte de intersectie ale graficelor celor 2 functii.
Observa ca x^2 are coeficient pozitiv deci Gf este o parabola cu ramurile in sus
Determini varful V(xv,yv) al parabolei Gf
Gg este o dreapta paralela cu abscisa
Faci o discutie :
m < yv rezulta Gf nu intersecteaza Gg
m = yv rezulta Gf intersectat cu Gg = {V}
m> yv rezulta Gf intersectat cu Gg = 2 puncte (cate un punct pe fiecare ramura a parabolei)
Altfel:
Numarul de puncte de intersectie este egal cu numarul de radacini reale ale ecuatiei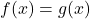
, de unde se obtine ecuatia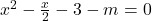 
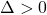), atunci sunt 2 puncte de intersectie.
), atunci avem un punct de intersectie.
), atunci nu avem puncte de intersectie.
Daca ecuatia are 2 radacini reale si distincte (
Daca ecuatia are radacinile reale si egale (
Daca ecuatia nu are radacini reale (
Va multumesc!