OLM 2013 Arad:
Fie a>0, a diferit de 1. Determinati functiile f:[0,1]–>R care indeplinesc simultan relatiile:
(i) | f(x) – f(y) |<=|a^x – a^y|, oicare x,y din [0,1]
(ii) {f(0) , f(1)} = {1,a}.
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
daca a>1 atunci avem 2 subcazuri:



 ,
,
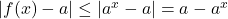




 deci
deci 
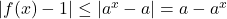


1.f(0)=1,f(1)=a.
din inegalitatea
punand y=0 atunci
deci
asadar
pe de alta parte din
deci
deci
din prima inegalitate obtinem ca
in concluzie
2.pentru f(0)=a,f(1)=1,punand
deci
pe de alta parte
deci
deci
deci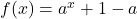
pentru cazul 2 in care
 si obtii
si obtii  etc.si aici
etc.si aici  obtinut in mod analog prin dubla inegalitate
obtinut in mod analog prin dubla inegalitate ……..
……..
se iau din nou subcazurile
2.1)
si cazul 2.2)