1. a). Sa se arate ca pt orice n apartine N* avem: k[x]<=[kx]<=k[x]+k-1 ,oricare ar fi x din R .
b) Daca pentru x din R .definim S(x)=[x]+[2x]+[4x]+[8x] sa se arate ca S(x) nu apartine intervalului (11,15) (oricare ar fi x real) iar apoi sa se rezolve in R ecuatia S(x)=1500014.
2. Sa se rezolve ecuatia in R: [(10x+1)/5]+[(10x+6)/5]=3[(10x-9)/5].
,unde [.] reprezinta partea intreaga.


1.![Rendered by QuickLaTeX.com [kx]=[k[x]+k\{x\}]=k[x]+[k\{x\}]](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-77c75e09ad27c236a0b9786b5ea340c6_l3.png) deoerece stim ca
deoerece stim ca ![Rendered by QuickLaTeX.com [x+k]=[x]+k,k\in Z](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-54db50436b167515da0a4807ecaffe8b_l3.png)
![Rendered by QuickLaTeX.com [k\{x\}]<[k]=k](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-ae879ec9e7a421753bd0cb0cb1d88b3c_l3.png) deci
deci ![Rendered by QuickLaTeX.com [k\{x\}]\leq k-1](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-1306866f8d17d1b50c85032766b3e3f4_l3.png)
de asemenea
de unde rezulta dubla inegalitate.
b)daca x<1,![Rendered by QuickLaTeX.com [x]\leq 0,[2x]\leq 1,[4x]\leq 3,[8x]\leq 7](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-779b22204be334d02150999886ba9385_l3.png) deci
deci ![Rendered by QuickLaTeX.com [x]+[2x]+[4x]+[8x]<1+3+7=11](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-f0709469d3187c77fa5653c4bb7ec39b_l3.png)
![Rendered by QuickLaTeX.com x\geq 1,[x]\geq 1,[2x]\geq 2,[4x]\geq 4,[8x]\geq 8\Rightarrow [tex][x]+[2x]+[4x]+[8x]\geq 15](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-3bf0a2f6dc0b85b259acbd9726e1055f_l3.png)
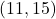
daca
deci suma de parti intregi nu poate fi in
Sau,putem folosi inegalitatea![Rendered by QuickLaTeX.com [2x]\leq 2[x]+1,[4x]\leq 4[x]+3,[8x]\leq 8[x]+7\Rightarrow [x]+[2x]+[4x]+[8x]\leq 15[x]+11](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-4ad67bb6fee6c92a3088ba3dbe02483b_l3.png) deci suma nu poate fi intre 11 si 15.
deci suma nu poate fi intre 11 si 15.
pentru a rezolva inecuatia,![Rendered by QuickLaTeX.com S(x)\geq 15[x]\geq 1500014](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-e7cb2f90c447c3545e519e99ca79ca5e_l3.png) deci
deci ![Rendered by QuickLaTeX.com [x]\leq 100000](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-f40a0ce23bb862ef82c54ef12aa704de_l3.png)
![Rendered by QuickLaTeX.com S(x)\leq 15[x]+11](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-860c891a926db1d6fbb0ddefde40fa87_l3.png) deci
deci ![Rendered by QuickLaTeX.com 1500014\leq 15[x]+11](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-4b9299f9bdfcd2e204bcce8f9db7c17b_l3.png) de unde
de unde ![Rendered by QuickLaTeX.com 1500003\leq 15[x]](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-2457679f055d5355a931a42ed9f7b6dc_l3.png) deci
deci ![Rendered by QuickLaTeX.com [x]\geq 100001](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-e58c28b2ede0d14d9b3338a70a93d624_l3.png) asadar ecuatia nu are solutii.
asadar ecuatia nu are solutii.
de asemenea
problema 2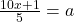 deci avem de rezolvat ecuatia:
deci avem de rezolvat ecuatia:
![Rendered by QuickLaTeX.com [a]+[a+1]=3[a-2]\Leftrightarrow [tex][a]+[a]+1=3[a]-6](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-43b0efbb04e578028357a45147e24bfb_l3.png) sau
sau ![Rendered by QuickLaTeX.com [a]=7](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-1c7c96933b2f731e1eca86cb9c6dbdd7_l3.png) deci
deci ![Rendered by QuickLaTeX.com \left[\frac{10x+1}{5}\right]=7](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-cd4364569215eeeea971579a8f28f82e_l3.png) de unde
de unde 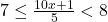 deci
deci 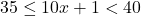 deci
deci 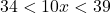 si ecuatia are solutii in intervalul
si ecuatia are solutii in intervalul 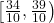
notam cu