![]()
Aratati ca sirul ![]() ,
, ![]()
este crescator si limita cand n tinde la infinit din ![]() este +infinit
este +infinit
Am aratat ca Imaginea functiei f este (0, infinit) si
am aratat ca sirul este crescator facand diferenta ![]()
Insa nu stiu unde ar trebui sa inlocuiesc sa demonstrez corect ca limita este inifinit …


trebuie sa ajungi la faptul ca deci
deci 
 rezulta ca
rezulta ca  deci
deci 
cum
La ce dai,la mate sau la info?
PS:poti folosi si criteriul raportului putin ajustat; atunci
atunci 

 nu rezulta neaparat ca sirul tinde la infinit!
nu rezulta neaparat ca sirul tinde la infinit! acest sir are limita……………..< infinit
acest sir are limita……………..< infinit
daca
ATENTIE insa la acel
Daca
Contraexemplu:pentru sirul cu proprietatea ca
astept din partea ta un raspuns la aceasta intrebare!
Revenind la problema noastra,daca demonstrezi ca
 rezulta folosind acest criteriu al raportului ca limita lui
rezulta folosind acest criteriu al raportului ca limita lui  e infinit.
e infinit.
iar
Prima rezolvare am inteles-o perfect, multumesc mult pentru ajutor. As mai avea o intrebare, totusi: , in cazul in care sirul nu este convergent ?
, in cazul in care sirul nu este convergent ?
Pt sirul ,
,
nu-mi dau seama care este limita, desi pare clar ca e finita pt. ca raportul tinde la 1.
Mai multe explicatii ale acestui criteriu al raportului ar fi binevenite.
La facultate dau la info, ma pricep mai bine acolo, ca la mate nu prea am avut noroc de profesori buni sau prea multa motivatie sa invat singur.
pai criteriul raportului functioneaza cand limita raportului e diferita de 1,daca aceasta exista.
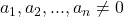
 e infinit.
e infinit.
iar aici,problema e cum nu se poate mai simpla;
aduci la acelasi numitor si obtii ca
bineinteles,trebuie si ca
deci limita sirului
Pardon, ma refeream la sirul pe care l-ati dat contraexemplu, . Inteleg ca, limita raportului fiind 1, => limita este finita.
. Inteleg ca, limita raportului fiind 1, => limita este finita.
 , dar nu stiu daca este >0 sau <0 ,
, dar nu stiu daca este >0 sau <0 ,  deci nu situ daca sirul este monoton.
deci nu situ daca sirul este monoton.
Pot afla limita?
deci contraexemplul meu nu e bun!