Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Aratati ca fractia 6n+7/10n+11 este ireductibila, oricare ar fi n∈ ℕ.
Eu am notat cu d=(6n+7,10n+11), adica cel mai mare divizor comun al celor doua numere
=> d|6n+7 =>d|30n+35
d|10n+11=>d|30n+33
le scadem si obtinem d|2.
In astfel de situatii obtineam d|1 si incheiam problema.Nu stiu totusi cum sa justific faptul ca fractia e ireductibila.
Please help!
Cum d|1 => d=1 => numaratorul si numitorul sunt numere naturale prime intre ele ,adica fractia este ireductibila .
Din d | 2 rezulta d E {1,2}
Este suficient sa precizam ca d E D(6n+7) iar 2 nu apartine D(6n+7) deoarece 6n+7 este numar impar rezulta d=1
unde D(6n+7)=multimea divizorilor lui 6n+7
demonstreaza ca fractia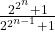
e ireductibila
Cu notatia 2^2^(n-1)=t obtinem 2^2^n=t^2
Fie d=(t^2+1,t+1) , deci d | t+1 (1)
si d | t^2 +1 (2)
Din (1) rezulta d | t^2 +t (3)
Din (2) si (3) rezulta d | t-1 (4)
Din (4) si (1) rezulta d | 2 (5)
Cum t+1 este impar rezulta 2 nu divide t+1 (6)
Din (1) , (5) si (6) rezulta d=1
Multumesc tuturor pentru explicatii!