Home/ Intrebari/Q 80041
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

captainjack
Pe: 2013-01-22T18:54:47+02:00 In: In:

Limita

Am incercat aici sa aplic limita remarcabila pt functiile trigonometrice, dar nu prea am ajuns la un rezultat convenabil in sensul ca tot in caz de nedeterminare sunt.

Similare

7 raspunsuri

  1. DD
    profesor

    Attached files

  2. captainjack

    DD, daca te uiti aici ( ), limita nu este infinit, ci 0 . Copiaza tot link-ul si pune-l pe tot in casuta de la browser ca altfel nu merge . Nu incerca sa contrazici raspunsul pt ca rezultatele sunt foarte precise pe site-ul asta 🙂

  4. PhantomR
    expert (VI)

    Probabil ca greseala e faptul ca lipeste minusul de la exponent in solutia domnului DD. Ar fi trebuit sa fie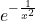 e^{-\frac{1}{x^2}}.

  5. ali
    maestru (V)

    Continui munca lui DD:
    \begin{array}{l} {\lim }\limits_{x \to 0} \frac{{x{e^{ - \frac{1}{{{x^2}}}}}}}{{t{g^2}x}} = \underbrace {{\lim }\limits_{x \to 0} \frac{{{x^2}}}{{t{g^2}x}}}_{ = 1} \times \frac{{{e^{ - \frac{1}{{{x^2}}}}}}}{x} = {\lim }\limits_{x \to 0} \frac{1}{{x{e^{\frac{1}{{{x^2}}}}}}} = L\\ \\ y = \frac{1}{x} \Rightarrow L = {\lim }\limits_{y \to \infty } \frac{y}{{{e^{{y^2}}}}}\\ \\ L = {\lim }\limits_{y \to \infty } \frac{y}{{{e^{{y^2}}}}} \Leftrightarrow \ln L = {\lim }\limits_{y \to \infty } \ln \frac{y}{{{e^{{y^2}}}}} = {\lim }\limits_{y \to \infty } \left( {\ln y - {y^2}} \right) = - \infty \Rightarrow L = {e^{ - \infty }} = 0\\ \\ \to {\lim }\limits_{x \to 0} \frac{{x{e^{ - \frac{1}{{{x^2}}}}}}}{{t{g^2}x}} = 1 \times 0 = 0 \end{array}
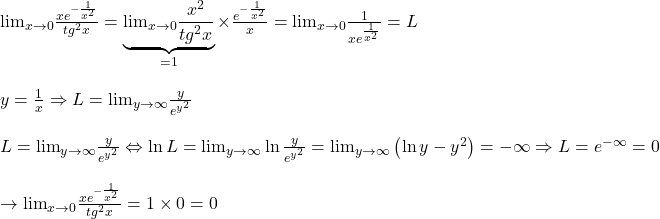
    De obicei, limite de genul ies imediat cu l’Hospital! (am presupus ca nu ai ajuns încă la aceasta regula)

  6. DD
    profesor

    SCUZE. Nu am fost atent ca exponentul lui e este -1/x^2. L-am luat cu +

  8. PhantomR
    expert (VI)

    ali wrote:
    {\lim }\limits_{y \to \infty } \left( {\ln y - {y^2}} \right) = - \infty

  9. ali
    maestru (V)

    y>=lny pentru y>=1 … ce sa mai zic de y când tinde la infinit …. !
    Apoi, noi avem y^2 >> y pentru y>=1.

    On-topic: problema se poate rezolva si cu criteriul clestelui (durează)…

Raspunde

Raspunde