Home/ Intrebari/Q 79975
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

Felicia_b
Pe: 2013-01-19T11:25:39+02:00 In: In:

limite de functii

1. Sa se calculeze:

    \[\begin{array}{l}a){\lim }\limits_{n \to \infty } \left( {\frac{{1!1 + 2!2 + ... + n!n}}{{(2n)! + 3}}} \right); \\ b){\lim }\limits_{x \to 0} \left( {\frac{{1 + 2^x + 3^x + ... + n^x }}{{n + 1}}} \right)^{\frac{1}{x}} . \\ \end{array}\]

2. Se considera functia f:R->R ,astfel incat:

    \[f(x) + 2f( - x) = \left\{ \begin{array}{l} x^2 ,\;x \le 0 \\ x,\;x > 0 \\ \end{array} \right.\]

a).Sa se studieze faca f are limita in x=0;
b) Sa se determine a,b din R pt care

    \[ {\lim }\limits_{x \to 1} \left( {x + a} \right) = 2\;si\ {\lim }\limits_{x \to - 1} f\left( {x + b} \right) = 1\]

Similare

8 raspunsuri

  1. sandy_sc
    maestru (V)

    Se noteaza cu an numaratorul fractiei si cu bn numitorul an, bn >0 bn–>oo atunci
    lim (an+1-an))/(bn+1-bn)=lm (an/bn)=
    continuarea in ataasament

  2. ali
    maestru (V)

    Problema 1-a)
    \begin{array}{l} \bullet \,k \times k! = \left( {k + 1 - 1} \right) \times k! = \left( {k + 1} \right)k! - k! = \left( {k + 1} \right)! - k!\\ \to \sum\limits_{k = 1}^n {k \times k!} = \sum\limits_{k = 1}^n {\left( {k + 1} \right)! - k!} = ... = \left( {n + 1} \right)! - 1\\ \to L = {\lim }\limits_{n \to \infty } \frac{{\sum\limits_{k = 1}^n {k \times k!} }}{{\left( {2n} \right)! + 3}} = {\lim }\limits_{n \to \infty } \frac{{\left( {n + 1} \right)! - 1}}{{\left( {2n} \right)! + 3}} = {\lim }\limits_{n \to \infty } \frac{{\left( {n + 1} \right)!}}{{\left( {2n} \right)! + 3}} - {\lim }\limits_{n \to \infty } \frac{1}{{\left( {2n} \right)! + 3}} = 0 - 0 = 0\\ \bullet \,\,\left( {2n} \right)! = \underbrace {1 \times 2 \times \cdots \times n \times \left( {n + 1} \right)}_{\left( {n + 1} \right)!} \times \cdots \times \left( {\underbrace {n + n}_{2n}} \right)\,\, > > \,\,\left( {n + 1} \right)! \end{array}

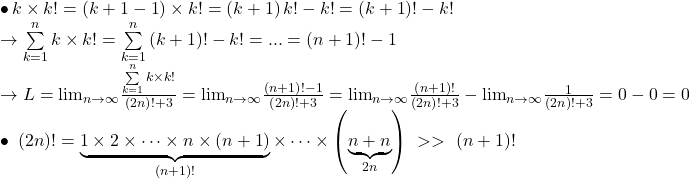
    Comentarii:
    Nu înteleg ce cauta 3 la numitor (este pus foarte aiurea) … din rezolvare mea, se vedea clar ca problema se putea restrânge mult mai elegant….

  4. ali
    maestru (V)

    Problema 1-b)
    \begin{array}{l} L = {\lim }\limits_{x \to 0} {\left( {\frac{{{1^x} + {2^x} + ... + {n^x}}}{{n + 1}}} \right)^{\frac{1}{x}}} \to {\rm{nedeterminare tip }}{1^\infty } \to {\rm{logaritmam:}}\\ \ln L = {\lim }\limits_{x \to 0} \ln {\left( {\frac{{{1^x} + {2^x} + ... + {n^x}}}{{n + 1}}} \right)^{\frac{1}{x}}} = {\lim }\limits_{x \to 0} \frac{{\ln \left( {{1^x} + {2^x} + ... + {n^x}} \right) - \ln \left( {n + 1} \right)}}{x}\\ {\rm{Aplicam teorema lui l'Hospital si obtinem:}}\\ \left\{ \begin{array}{l} \frac{{d\left[ {\ln \left( {{1^x} + {2^x} + ... + {n^x}} \right) - \ln \left( {n + 1} \right)} \right]}}{{dx}} = \frac{{{2^x}\ln 2 + ... + {n^x}\ln n}}{{{1^x} + {2^x} + ... + {n^x}}} - 0\\ \frac{{d\left( x \right)}}{{dx}} = 1 \end{array} \right. \Rightarrow \\ \ln L = {\lim }\limits_{x \to 0} \frac{{{2^x}\ln 2 + ... + {n^x}\ln n}}{{{1^x} + {2^x} + ... + {n^x}}} = {\lim }\limits_{x \to 0} \frac{{{{\left( {\frac{2}{n}} \right)}^x}\ln 2 + {{\left( {\frac{3}{n}} \right)}^x}\ln 3 + ... + \ln n}}{{{{\left( {\frac{1}{n}} \right)}^x} + {{\left( {\frac{2}{n}} \right)}^x} + ... + 1}}\\ = \frac{{\ln n!}}{n} \Leftrightarrow \ln L = \ln \sqrt[n]{{n!}} \Rightarrow L = \sqrt[n]{{n!}} \end{array}

    Comentarii:
    Aceasta problema este creata dintr-o alta problema (deci, autorul problemei nu are nici un merit)…. Intra-adevăr, în zilele noastre, se fac culegeri de matematica nu din teorie ci din alte culegeri … lucru lamentabil.
    Nu înteleg de ce autorul a ales n+1 la numitor în loc de n (prostie)!
    Problema se mai poate rezolva folosind criteriul clestelui … însă durează!

  5. sandy_sc
    maestru (V)

    Problema2

    Din calcule se ajunge la n edeterminaare 1^oo.
    Se prluctreaza limta aduunad si scazzand 1, a.i sa ajungem:

  6. Felicia_b

    Va multumesc mult!! 🙂
    Domnul Ali, problema 1-b) este din manualul Burtea-XI ..dar este data la capitolul ”limite de functii” ..inca nu am facut regulile lui l’Hospital.
    Plus..daca se mai poate inca o intrebare..
    Sa se calculeze urmatoarea limita:

        \[ {\lim }\limits_{x \to \infty } \left( {x \cdot \sin \frac{1}{x}} \right)\]

    M-am gandit sa scriu

        \[ {\lim }\limits_{x \to \infty } \left( {x \cdot \sin \frac{1}{x}} \right) ={\lim }\limits_{x \to \infty } \frac{{\sin \frac{1}{x}}}{{\frac{1}{x}}} = 1\]

    .
    Este bine? am ceva confuzii din prisma faptului ca limita fundamentala este de obicei in cazul cand x->0 dar acum x tinde la oo.
    Afecteaza acest lucru in exercitiul dat?

  8. sandy_sc
    maestru (V)

    f(o)-2f(o)=o^2=0 => f(0)=0
    X–>0, X<0 limf(x)= 0^2=0
    X–>0 X>0 limf(x)=0 (f(x)=x)
    ASadar in0 avem ls=ld =f(0) uncia are liimita in 0

  9. ali
    maestru (V)

    Da în mare parte e bine …. mai pe înteles: notam t=1/x atunci:
    {\lim }\limits_{x \to \infty } \left( {x\sin \frac{1}{x}} \right) = {\lim }\limits_{t \to 0} \frac{{\sin t}}{t} = 1
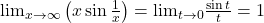
    Limita remarcabila pe care o sti tu!
    Atentie însă la modificări (atunci când am făcut trecerea de la x la t)….
    sandy_sc … referitor la problema 1-b) nu cred ca este bine cum ai făcut (atentie la teorie) !

  10. ghioknt
    profesor

    Nu stiu daca te mai intereseaza subiectele, dar le abordez pentru ca am observat unele inadvertente in raspunsurile pe care le-ai primit.
    In primul rand la 1b) nu exista nicio nedeterminare pentru ca limita bazei nu este 1, ci n/(n+1), adica un numar subunitar. Asta a fost
    intentia autorului cand a schimbat n cu n+1, sa evite aparitia prematura a unei nedeterminari. Apoi, despre exponentul 1/x stim ca
    nu are limita in 0, ci doar limite laterale diferite: la stanga -oo, la dreapta +oo. Operatiile cu limite conduc asadar, la rezultatele:
    la stanga [n/(n+1)]^-oo=+oo; la dreapta [n/(n+1)]^+oo=0; limita,asa cum este ea scrisa de tine, nu exista.
    2)E usor de aratat ca f(0)=0, dar nu stiu sa arat ca exista limite laterale in 0, fara sa aflu expresiile lui f.
    Fie x<0; atunci f(x)+2f(-x)=x^2 ;
    dar -x>0, deci f(-x)+2f(x)=-x .
    Din acest sistem aflam ,,necunoscutele” f(x) si f(-x): f(x)=(-x^2-x)/3, care este expresia lui f pentru x<0; f(-x)=(2x^2+x)/3
    in care schimbam pe -x cu x si obtinem f(x)=(2x^2-x)/3, adica expresia lui f pentru x>0.
    Acum este clar ca limitele laterale in 0 exista si sunt 0. Mai mult acum stim ca f este continua pe R si deci celelalte 2 limite
    din problema sunt, de fapt, 2 valori: f(1+a)=2, f(-1+b)=1. Observam insa ca prima restrictie a lui f are un maxim=1/3 (pt x=-1),
    deci nu poate lua valorile 2 sau 1. A doua restrictie are un minim=-1/24 (pt. x=1/4), deci poate lua cele 2 valori.
    f(x)=2, adica (2x^2-x)/3=2 are o radacina pozitiva 2, deci 1+a=2,da a=1; la fel f(x)=1 are o radacina pozitiva 3/2, -1+b=3/2 da b=5/2.
    Cu bine, ghioknt.

Raspunde

Raspunde