Home/ Intrebari/Q 79855
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

gixgex
Pe: 2013-01-13T15:41:57+02:00 In: In:

numere complexe

1.
Z apartine C\R
aflati minimul :
Im(Z^5)/(Im Z)^5

2.
Z apartine C
|z|=1
aratati ca:
|z+1|+|z^2+1|+|z^3+1|>=2

3.
daca
|z1+z2|=sqrt(3)
|z1|=|z2|=1
aratati ca:
|z1-z2|=1

nu stiu din ce carte sunt problemele deoarece profesorul le-a dictat.

Similare

4 raspunsuri

  1. gunty
    maestru (V)

    1.

    Fie

        \[ z = a + bi;b \ne 0 \Rightarrow \]

    [tex]\[
    \frac{{{{\rm Im}\nolimits} z^5 }}{{\left( {{{\rm Im}\nolimits} z} \right)^5 }} = \frac{{{{\rm Im}\nolimits} \left( {a + bi} \right)^5 }}{{\left[ {{{\rm Im}\nolimits} \left( {a + bi} \right)} \right]^5 }}
    \][/tex]

    Se calculeaza, ca

        \[ \left( {a + bi} \right)^5 = a^5 + 5ab^4 - 10a^3 b^2 + i\left( {b^5 + 5a^4 b - 10a^2 b^3 } \right) \]

    . Deci avem:

        \[ \frac{{{{\rm Im}\nolimits} \left( {a + bi} \right)^5 }}{{\left[ {{{\rm Im}\nolimits} \left( {a + bi} \right)} \right]^5 }} = \frac{{b^5 + 5a^4 b - 10a^2 b^3 }}{{b^5 }} = 1 + 5\frac{{a^4 }}{{b^4 }} - 10\frac{{a^2 }}{{b^2 }} = 5\left( {\frac{{a^2 }}{{b^2 }}} \right)^2 - 10\frac{{a^2 }}{{b^2 }} + 1 \]

    Fie

        \[ t = \frac{{a^2 }}{{b^2 }} \]

    , si primim

        \[ 5\left( {\frac{{a^2 }}{{b^2 }}} \right)^2 - 10\frac{{a^2 }}{{b^2 }} + 1 = 5t^2 - 10t + 1 \]

    Sa demonstram, ca

        \[ 5t^2 - 10 \cdot t + 1 \ge - 4 \]

    :

        \[ 5t^2 - 10 \cdot t + 1 \ge - 4 \Leftrightarrow 5t^2 - 10 \cdot t + 5 \ge 0 \Leftrightarrow t^2 - 2t + 1 \ge 0 \Leftrightarrow \left( {t - 1} \right)^2 \ge 0_{(adev.)} \]

    In concluzie,

        \[ \min \left( {\frac{{{{\rm Im}\nolimits} z^5 }}{{\left( {{{\rm Im}\nolimits} z} \right)^5 }}} \right) = - 4 \]

    .

    * Mentionez, ca

        \[ \frac{{{{\rm Im}\nolimits} z^5 }}{{\left( {{{\rm Im}\nolimits} z} \right)^5 }} = - 4 \]

    are loc pentru Im(z)=Re(z).

  2. gixgex

    multumesc

  4. ali
    maestru (V)

    Problema 3: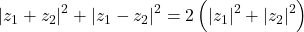
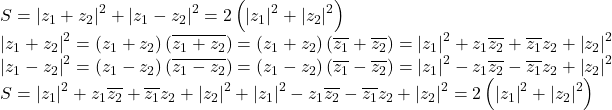
    Vom folosi aceasta identitate: {\left| {{z_1} + {z_2}} \right|^2} + {\left| {{z_1} - {z_2}} \right|^2} = 2\left( {{{\left| {{z_1}} \right|}^2} + {{\left| {{z_2}} \right|}^2}} \right)
    Demonstratia identităti:
    \begin{array}{l} S = {\left| {{z_1} + {z_2}} \right|^2} + {\left| {{z_1} - {z_2}} \right|^2} = 2\left( {{{\left| {{z_1}} \right|}^2} + {{\left| {{z_2}} \right|}^2}} \right)\\ {\left| {{z_1} + {z_2}} \right|^2} = \left( {{z_1} + {z_2}} \right)\left( {\overline {{z_1} + {z_2}} } \right) = \left( {{z_1} + {z_2}} \right)\left( {\overline {{z_1}} + \overline {{z_2}} } \right) = {\left| {{z_1}} \right|^2} + {z_1}\overline {{z_2}} + \overline {{z_1}} {z_2} + {\left| {{z_2}} \right|^2}\\ {\left| {{z_1} - {z_2}} \right|^2} = \left( {{z_1} - {z_2}} \right)\left( {\overline {{z_1} - {z_2}} } \right) = \left( {{z_1} - {z_2}} \right)\left( {\overline {{z_1}} - \overline {{z_2}} } \right) = {\left| {{z_1}} \right|^2} - {z_1}\overline {{z_2}} - \overline {{z_1}} {z_2} + {\left| {{z_2}} \right|^2}\\ S = {\left| {{z_1}} \right|^2} + {z_1}\overline {{z_2}} + \overline {{z_1}} {z_2} + {\left| {{z_2}} \right|^2} + {\left| {{z_1}} \right|^2} - {z_1}\overline {{z_2}} - \overline {{z_1}} {z_2} + {\left| {{z_2}} \right|^2} = 2\left( {{{\left| {{z_1}} \right|}^2} + {{\left| {{z_2}} \right|}^2}} \right) \end{array}

    Revin la problema:
    {\left| {{z_1} - {z_2}} \right|^2}\, = \limits^{{\rm{conform identitati}}} \,2\left( {{{\left| {{z_1}} \right|}^2} + {{\left| {{z_2}} \right|}^2}} \right) - {\left| {{z_1} + {z_2}} \right|^2} = 2 \times 2 - 3 = 1
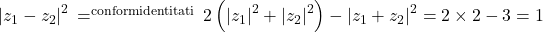
    Problema 2 a fost rezolvata pe un alt forum de matematica !!!

  5. gixgex

    multumesc

Raspunde

Raspunde