Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
1. Sa se studieze convergenta sirurilor (an) si (bn) :
![\[a_n = \frac{{\left( {n - 3} \right)^2 }}{{n^2 + 1}}\;\;;b_n =\frac{{( - 1)^n \cdot n}}{{n + 2}}\]](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-bbf9b47fdfe13ac6aca39a0d630ccc92_l3.png "Rendered by QuickLaTeX.com")
2. Sa se arate ca urmatoarele siruri (an) au cel putin un subsir convergent si sa se dea un exemplu de asemenea subsir:
![\[a)\;\;a_n = \frac{{n + \left( { - 1} \right)^n }}{{n + 1}};\;\;\;b)\;a_n = \cos \frac{{(n + 1)\pi }}{4};\quad c)\;a_n = \sin \frac{{n\pi }}{4} \cdot \cos \frac{{n\pi }}{3}\]](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-e656ffd2f7e541d8fc6ab5e25751a74e_l3.png "Rendered by QuickLaTeX.com")
3. Se considera sirul
![\[\left( {x_n } \right)_{n \ge 0} \]](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-4d6f26a5e368358069206ec681c7c1ad_l3.png "Rendered by QuickLaTeX.com")
si cu
![\[x_0 \in \left( {0,1} \right)\]](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-22d9d34ff5fb90a65b0de82bfca7a4e3_l3.png "Rendered by QuickLaTeX.com")
si
![\[x_{n + 1} = x_n - x_n ^2 \]](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-1cc370cbd88bc7bc0971a23849e2d491_l3.png "Rendered by QuickLaTeX.com")
. Sa se studieze monotonia si marginirea si sa afle limita, daca aceasta exista.
In cazul cad sirrul re l numitor si numarator,polinoame in n,avand acelasi grad, ptdterminnare llimitei se face raportul termenilor de grd cel mai inalt
In cazul tau ridici pe (n-3) la patraat si faci raportul coefcientilor lui n^2
de l numarrator si numitr((1/1=1)
deci an tinde la 1
bn Se obserbva ca pt n =2k ((n par) obii subsiruul b2k=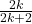
Candd K–>+oo conf regulii de mai ssus b2k –>1
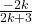care tinde la -1
Pt n=2k+1 (n=impar) 0btii subsirul
b2k+1=
SSirul bn contine 2 subsiruri avannd limite diferrite, deci e diverrget
eX2
atasameent