Home/ Intrebari/Q 79620
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

budulica
Pe: 2012-12-23T11:25:51+02:00 In: In:

inegalitate

Fie a,b,c\epsilon \mathbb{R}_{+} . Demonstrati ca, daca a+b+c=3, atunci \sqrt{3a+1}+\sqrt{3b+1}+\sqrt{3c+1}< \frac{15}{2}

multumesc!!

Similare

5 raspunsuri

  1. ali
    maestru (V)

    \begin{array}{l} {\left( {MA - MG} \right)_2}:\,\sqrt {3a + 1} = \sqrt {1 \times \left( {3a + 1} \right)} \le \frac{{1 + 3a + 1}}{2} = \frac{{3a + 2}}{2}\\ {\rm{Idem}} \Rightarrow \sum {\sqrt {3a + 1} } \le \frac{{3a + 2 + 3b + 2 + 3c + 2}}{2} = \frac{{3\left( {\overbrace {a + b + c}^{ = 3}} \right) + 6}}{2} = \frac{{9 + 6}}{2} = \frac{{15}}{2} \end{array}

  2. mihai2000

    Avem, din inegalitatea mediilor, media geometrica <= media aritmetica
    {M}_{g}\leq {M}_{a}
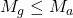
    Putem lua cei doi termeni, 3a+1 si 1, si avem:

    \sqrt{(3a+1)(1)}\leq \frac{(3a+1) + 1}{2}

    La fel se procedeaza pentru b si c si se aduna cele trei inegalitati.
    Cu conditia a+b+c = 3 nu putem avea 3a+1 = 1, 3b+1 = 1 si 3c+1 = 1 simultan, deci inegalitatea finala este stricta.

    Scuze, ali, scriam in timp ce a aparut soluta ta (mai eleganta) …

  4. petrut5

    budulica wrote: Fie a,b,c\epsilon \mathbb{R}_{+} . Demonstrati ca, daca a+b+c=3, atunci \sqrt{3a+1}+\sqrt{3b+1}+\sqrt{3c+1}< \frac{15}{2}

    multumesc!!

    \rm{\Large \bl 3a+1=x, 3b+1=y, 3c+1=z\\\;\\x+y+z=3(a+b+c)+3 \Rightarrow x+y+z=3\cdot3+3=12.\\\;\\(\sqrt x+\sqrt y+sqrt z)^2=x+y+z+2(\sqrt{xy}+\sqrt{yz}+\sqrt{zx}) \leq12+2(x+y+z) \Rightarrow\\\;\\\Rightarrow (\sqrt x+\sqrt y+\sqrt z)^2\leq12+2\cdot12 \Rightarrow (\sqrt x+\sqrt y+\sqrt z)^2 \leq 36 \Rightarrow \sqrt x+\sqrt y+\sqrt z \leq6 < \frac{15}{2}}

  5. Darstar

    Totusi unde s-a pierdut cazul de egalitate?

    Attached files

  6. ali
    maestru (V)

    Când am rezolvat prima data problema am crezut ca este vorba de \le … încă si cred! …. fiindcă aproape toate problemele de genul (evident, cele întâlnite de mine) contin \le (m-am gândit ca ,budulica, nu a dat mare importanta semnului si l-a trecut cum a vrut, multi încă confunda inegalitate cu inecuatia).
    In cazul în care semnul, într-adevăr, se dovedeste a fi < si nu \le …atunci rezolvarea mea nu este cea potrivita…..
    Probabil era mai corect sa întreb autorul despre semn!

Raspunde

Raspunde