Home/ Intrebari/Q 79598
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

Deny95
Pe: 2012-12-19T14:28:03+02:00 In: In:

Inegalitate grea!

a^2+b^2+c^2=3, a,b,c>=0. Sa se arate ca (a^3+a+1)(b^3+b+1)(c^3+c+1)<=27.
Este o problema dintre cele propuse in gazeta 11/2012.
Rog mult ajutor din partea celor cu experienta…

Similare

8 raspunsuri

  1. Zeus
    veteran (III)

    \frac{a^3+a+1}{3}*\frac{b^3+b+1}{3}\leq \frac{a^3*b^3+a*b+1}{3}Inmultim cu (c^3+c+1) si mai aplicam o data Cebasev.\frac{a^3*b^3+a*b+1}{3}*\frac{c^3+c+1}{3}\geq \frac{(a^3+a+1)*(b^3+b+1)*(c^3+c+1)}{27}=>(a^3+a+1)*(b^3+b+1)*(c^3+c+1)\leq 9*(a^3*b^3*c^3+a*b*c+1)...a^2+b^2+c^2=3=>\frac{a^2+b^2+c^2}{3}\geq \sqrt[3]{a^2*b^2*c^2}<=>abc\leq 1. Inlocuim sus si ne da inegalitatea ceruta!

  2. Deny95

    Multumesc!

  4. Deny95

    Dar ca sa pot aplica Cebisev nu trebuia sa stiu ceva de monotonia sirurilor a, a^3, 1 si omoloagele?

  5. Zeus
    veteran (III)

    a cu b, a^3 cu b^3 au acelasi semn.
    Caz I a<=b =>a^3<=b^3.
    Caz II a>b =>a^3>=b^3.
    La fel si dincolo
    a*b cu c si a^3*b^3 cu c^3. E clar?

  6. Deny95

    Eu stiam asa:
    Daca a1,a2,a3,….,an si b1,b2,b3,…,bn sunt la fel monotone, atunci:
    (a1+a2+a3….+an)(b1+b2+b3+….+bn)<=n(a1b1+a2b2+….anbn).
    Nu asta este ineg lui Cebasev?
    Daca da, nu trebuie ca a^3,a si 1 ca sir si b^3,b si 1 sa fie la fel monotone?

  8. Zeus
    veteran (III)

    Ai dreptate m-am grabit! Aplica ln in fiecare parte… si apoi considera functia f(x)=ln(x^3+x+1)… care cred ca e concava… si aplici f(x)+f(y)+f(z)<=3*f((x+y+z)/3)). Ia vezi iese ceva?

  9. ali
    maestru (V)

    Sirurile a_i si b_i trebuie ordonata astfel:
    \begin{array}{l} \left( {{a_1} < {a_2} < {a_3}} \right) \wedge \left( {{b_1} < {b_2} < {b_3}} \right)\\ \vee \left( {{a_1} > {a_2} > {a_3}} \right) \wedge \left( {{b_1} > {b_2} > {b_3}} \right) \end{array}
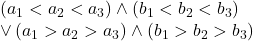
    Este simplu în rest ….
    Ai cazul în care a,b<1 => primul caz….
    Sau a,b>1=> al 2 caz….
    Deci putem aplica Cebasev!
    Dar de unde stim ca a, b au acelasi semn(adică se comporta la fel)… ? simplu … rezulta dintr-o alta inegalitate (o inegalitate pornita din conditia initială)!
    Mai multe detalii citesti aici : http://forum.matematic.ro/viewtopic.php?t=21998
    Ps: am picat de 100 de ori în capcana …. este interzis (nu este fairplay fata de alti) sa rezolvam topic-uri propuse de anumite concursuri…. Cel mai bun scenariu este sa indicam o directie propunătorului!

  10. Zeus
    veteran (III)

    Domnule Ali … nu vreau sa ma contrazic cu matale dar e cam lunga demonstratia asta cu cazuri etc… cred ca mai bine bagam ln-ul in functiune.

Raspunde

Raspunde