Home/ Intrebari/Q 79360
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

captainjack
Pe: 2012-12-04T13:16:40+02:00 In: In:

Calculul unor limite

Ma puteti ajuta cu niste calcule ale unor limite, va rog ?

,unde n tinde in toate exercitiile la infinit, a, b, c sunt numere reale si am notat cu {x} = partea fractionara a numarului x .

Daca nu stiti raspunsurile la toate exercitiile, scrieti solutiile doar pt exercitiile pe care le-ati rezolvat.

Edit : la exercitiul 2), nu este e la puterea (n+1), ci doar e la puterea n + 1 separat

Similare

5 raspunsuri

  1. ali
    maestru (V)

    Prima problema
    \begin{array}{l} L = {\lim }\limits_{n \to \infty } \left\{ {\sqrt {{n^2} + 2n} } \right\}\\ \left\{ {\sqrt {{n^2} + 2n} } \right\} = \sqrt {{n^2} + 2n} - \left\lfloor {\sqrt {{n^2} + 2n} } \right\rfloor \\ n = \left\lfloor {\sqrt {{n^2}} } \right\rfloor < \left\lfloor {\sqrt {{n^2} + 2n} } \right\rfloor < \left\lfloor {\sqrt {{n^2} + 2n + 1} } \right\rfloor = n + 1 \Rightarrow \left\lfloor {\sqrt {{n^2} + 2n} } \right\rfloor = n\\ L = {\lim }\limits_{n \to \infty } \sqrt {{n^2} + 2n} - n = 1 \end{array}
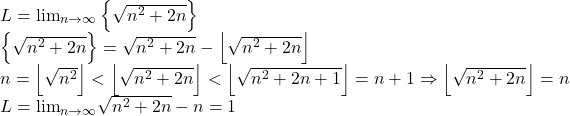
    Modul de rezolvare a ultimei limite este foarte cunoscut!

  2. ali
    maestru (V)

    Problema 2:
    \begin{array}{l} L = {\lim }\limits_{n \to \infty } \frac{{{2^n}}}{{{e^n} + 1}} = {\lim }\limits_{n \to \infty } \frac{1}{{{{\left( {\frac{e}{2}} \right)}^n} + \frac{1}{{{2^n}}}}} = \frac{1}{{{\lim }\limits_{n \to \infty } {{\left( {\frac{e}{2}} \right)}^n} + \frac{1}{{{2^n}}}}}\\ \left\{ \begin{array}{l} {\lim }\limits_{n \to \infty } {\left( {\frac{e}{2}} \right)^n} = \infty \\ {\lim }\limits_{n \to \infty } {\left( {\frac{1}{2}} \right)^n} = 0 \end{array} \right. \Rightarrow L = \frac{1}{\infty } = 0 \end{array}
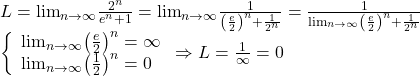
    Idem cealaltă limita !

  4. ali
    maestru (V)

    Problema 3…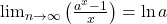
    Se aplica formula pentru limita remarcabila: {\lim }\limits_{n \to \infty } \left( {\frac{{{a^x} - 1}}{x}} \right) = \ln a
    Deocamdată, am rezolvat problema printr-un procedeu mai lung …. rezultatul este sqrt_3(abc) …. Voi posta solutia dacă vad ca nu primiti vreo rezolvare (mai scurta) de la un alt membru !

  5. captainjack

    mersi, am reusit sa le rezolv, dar mai am o limita pe care nu am reusit s-o calculez ..

    daca poti, te rog, sa ma ajuti..

    Edit : l-am rezolvat si pe asta ; aia nu era partea intreaga si asta m-a derutat . Multumesc mult pentru rezolvari, ali 😀

  6. DD
    profesor

    Limita data se poate pune sub forma; lim(n->infnit) din ln[(1+(2/n^2))/(1+(1/n^2))]^(n^2)=ln(e^2/e)=1
    Limita 3)lim(n->infinit) din{ [(a^(1/n)+b^(1/n)+c^(1/n)]/3}^n=lim(n->inf.)din {[(1+(lna)/n)+(1+(lnb)/n)+(1+lnc)/n)]/3}^n=lim(n->inf.)din
    [(3+(ln(a.b.c))/n)/3]^n=lim(n->inf.) din{[1+(ln(al 3-a radical din a.b.c))]/n}^n=(al 3-a radical din a.b.c)
    Lim.4)(1/((e^n)+1))^(1/n)=(1/e).1/(1+(1/e^n))^(1/n)=1/e
    lim 1)Ilimita este bine facuta pana la=1={1,0}=0

Raspunde

Raspunde