Home/ Intrebari/Q 79325
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

dennis9091
guru (IV)
Pe: 2012-12-02T14:48:06+02:00 In: In:

Inegalitate.

Sa se demonstreze ca :
1+ (1/2^3) + (1/3^3) + … + (1/2005^3) < 5/4. Generalizare.

Similare

7 raspunsuri

  1. ali
    maestru (V)

    Problema este foarte anevoioasa … o posibila solutie ar fi :
    \begin{array}{l} S = 1 + \frac{1}{{{2^3}}} + \frac{1}{{{3^3}}} + ... + \frac{1}{{{n^3}}}\\ {k^3} > {k^3} - k = k\left( {{k^2} - 1} \right) \Rightarrow \frac{1}{{{k^3}}} < \frac{1}{{k\left( {{k^2} - 1} \right)}} = \frac{1}{2}\left( {\frac{1}{{k - 1}} + \frac{1}{{k + 1}} - \frac{2}{k}} \right)\\ = \frac{1}{2}\left( {\frac{1}{{k + 1}} - \frac{1}{k} + \frac{1}{{k - 1}} - \frac{1}{k}} \right) \end{array}
    \begin{array}{l} \sum\limits_{k = 1}^n {\frac{1}{{{k^3}}}} < 1 + \frac{1}{2} \times \sum\limits_{k = 2}^n {\left( {\frac{1}{{k - 1}} - \frac{1}{k} + \frac{1}{{k + 1}} - \frac{1}{k}} \right)} \\ = 1 + \frac{1}{2}\left( {\sum\limits_{k = 2}^n {\frac{1}{{k - 1}} - \frac{1}{k}} + \sum\limits_{k = 2}^n {\frac{1}{{k + 1}} - \frac{1}{k}} } \right) = 1 + \frac{1}{2}\left( {\frac{{n - 1}}{n} + \frac{1}{{n + 1}} - \frac{1}{2}} \right)\\ = 1 + \frac{{\left( {n - 1} \right)\left( {n + 2} \right)}}{{4n\left( {n + 1} \right)}}\\ n = 2005 \Rightarrow {S_{2005}} < 1 + \frac{{2004 \times 2007}}{{4 \times 2005 \times 2006}} \approx 1.249 < \frac{5}{4} = 1.25 \end{array}

    Dupa cum vezi … am început mai întâi cu generalizarea mai apoi cu solutia urmărită …..
    Ps1: Pentru cei care stiu ce înseamnă limita …. pentru n= infinit => S<lim(din acea fractia) care este tocmai 5/4.
    Ps2: Daca se dovedesti ca aceasta problema este una propusa la GM atunci nu vei mai primi de la mine(cel putin) nici o solutie vreodată !

  2. Integrator
    maestru (V)

    dennis9091 wrote: Sa se demonstreze ca :
    1+ (1/2^3) + (1/3^3) + … + (1/2005^3) < 5/4. Generalizare.


    Notăm S=\sum_{k=1}^n{\frac{1}{k^3}}.Putem scrie următoarea inegalitate \frac{1}{k^3}<\frac{1}{2 \cdot (k-1)^2}-\frac{1}{2 \cdot k^2} care se demonstrează foarte uşor deoarece această inegalitate se deduce rapid din inegalitatea \frac{k-2}{k}<\frac{k}{k-1}.
    Dând valori lui k=2,3,4,.........,n-1,n obţinem urmatoarele egaltăti şi inegalităti:
    1=1

    \frac{1}{2^3}=\frac{1}{4}-\frac{1}{2 \cdot 2^2}<\frac{1}{2}-\frac{1}{2 \cdot 2^2}

    \frac{1}{3^3}<\frac{1}{2 \cdot 2^2}-\frac{1}{2 \cdot 3^2}

    \frac{1}{4^3}<\frac{1}{2 \cdot 3^2}-\frac{1}{2 \cdot 4^2}
    –––––––––––––––––––––––––––-
    –––––––––––––––––––––––––––
    \frac{1}{(n-1)^3}<\frac{1}{2 \cdot (n-2)^2}-\frac{1}{2 \cdot (n-1)^2}

    \frac{1}{n^3}<\frac{1}{2 \cdot (n-1)^2}-\frac{1}{2 \cdot n^2}

    Făcând suma rezultă că S=\sum_{k=1}^n{\frac{1}{k^3}} \leq 1+\frac{1}{4}-\frac{1}{2 \cdot n^2}=\frac{5}{4}-\frac{1}{2 \cdot n^2} pentru orice valori de numere naturale n \geq 2

    egalitatea având loc pentru n=2.În cosecinţă S=\sum_ {k=1}^n{\frac{1}{k^3}}<\frac{5}{4}.
    Evident că orice sumă parţială şi deci si cea pentru care n=2005 este mai mică decât \frac{5}{4}.

  4. ali
    maestru (V)

    In primul rând acea inegalitate nu este valabila pentru k=1 …. hai sa zicem ca fortăm suma si pornim de la 2 (desi nu este tocmai corect sa porneste de la o inegalitate care contine o mica eroare … desi poate iti da un rezultat corect ….)
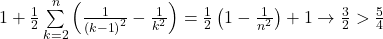
    In al 2 rând, suma :
    1 + \frac{1}{2}\sum\limits_{k = 2}^n {\left( {\frac{1}{{{{\left( {k - 1} \right)}^2}}} - \frac{1}{{{k^2}}}} \right)} = \frac{1}{2}\left( {1 - \frac{1}{{{n^2}}}} \right) + 1 \to \frac{3}{2} > \frac{5}{4}
    Dupa cum vezi, am pornit suma de la 2 fiindcă în punctul k=1 apare singularitate !
    Ma rog, poate nu am înteles bine despre ce suma este vorba !

  5. bedrix
    expert (VI)

    Intrucat limitele nu sunt in programa de clasa a VIII-a sa continuam prin metoda propusa de Ali , adaptata nivelului de cl. a VIII-a.
    Problema se reduce la a arata ca S=1/2^3 +….+1/2005^3<1/4
    Avem 1/2^3<(1/2)*(1/1 +1/3 -2/2)
    1/3^3<(1/2)*(1/2 +1/4 -2/3)
    1/4^3<(1/2)*(1/3 +1/5 -2/4)
    …….
    1/2003^3<(1/2)*(1/2002 +1/2004 -2/2003)
    1/2004^3<(1/2)*(1/2003 +1/2005 -2/2004)
    1/2005^3<(1/2)*(1/2004 +1/2006 -2/2005)
    Adunam inegalitatile si rezulta S<(1/2)*(1-1/2 +1/2006 -1/2005)=1/4 -1/(2*2005*2006)<1/4

  6. Integrator
    maestru (V)

    La limită pentru k \to 1 acea inegalitate rămâne valabilă.
    Atenţie la ineglitatea \frac{1}{2^3}=\frac{1}{4}-\frac{1}{2 \cdot 2^2}<\frac{1}{2}-\frac{1}{2 \cdot 2^2}……şi făcând suma egalităţilor în aşa fel încât în cazul k=2 folosesc egalitatea \frac{1}{2^3}=\frac{1}{4}-\frac{1}{2 \cdot 2^2} atunci rezultă că S \leq 1+\frac{1}{4}-\frac{1}{2 \cdot n^2}……a se vedea că suma pentru n=2 este chiar egală cu \frac{9}{8} adică nu există o inegalitate strictă pentru orice vloare naturală a lui n.Încă odata rog a se citi modul cum am făcut sumarea.

  8. ali
    maestru (V)

    Integrator: asta ai scris tu:
    \begin{array}{l} \frac{1}{{{k^3}}} < \frac{1}{2}\left( {\frac{1}{{{{\left( {k - 1} \right)}^2}}} - \frac{1}{{{k^2}}}} \right)\\ 1 = 1\\ \frac{1}{{{2^3}}} < \frac{1}{2} - \frac{1}{{2\cdot{2^2}}}\\ \frac{1}{{{3^3}}} < \frac{1}{{2\cdot{2^2}}} - \frac{1}{{2\cdot{3^2}}}\\ \frac{1}{{{4^3}}} < \frac{1}{{2\cdot{3^2}}} - \frac{1}{{2\cdot{4^2}}}\\ - - - - - - - - - - - - - \\ - - - - - - - - - - - - - \\ \frac{1}{{{{(n - 1)}^3}}} < \frac{1}{{2\cdot{{(n - 2)}^2}}} - \frac{1}{{2\cdot{{(n - 1)}^2}}}\\ - - - - - - - \\ 1 + \sum\limits_{k = 2}^n {\frac{1}{{{k^3}}} < 1 + \frac{1}{2}\sum\limits_{k = 2}^n {\frac{1}{{{{\left( {k - 1} \right)}^2}}} - \frac{1}{{{k^2}}}} } \end{array}
    Oricum le-ai lua acele sume (scrise una sub alta) sunt egale cu:
    \frac{1}{2}\left( {1 - \frac{1}{{2{n^2}}}} \right) + 1 \ne \frac{5}{4} - \frac{1}{{2{n^2}}}

  9. bedrix
    expert (VI)

    Generalizare
    Problema se reduce la a arata ca S=1/2^3 +….+1/n^3<1/4
    Avem 1/2^3<(1/2)*(1/1 +1/3 -2/2)
    1/3^3<(1/2)*(1/2 +1/4 -2/3)
    1/4^3<(1/2)*(1/3 +1/5 -2/4)
    …….
    1/(n-1)^3<(1/2)*(1/(n-2) +1/n -2/(n-1))
    1/n^3<(1/2)*(1/(n-1) +1/(n+1) -2/n)
    Adunam inegalitatile si rezulta S<(1/2)*(1-1/2 +1/(n+1) -1/n)=1/4 -1/(2*n*(n+1))<1/4

Raspunde

Raspunde