Am intampinat niste probleme in rezolvarea acestor 2 ex.Sa se studieze convergenta sirurilor:
Multumesc anticipat!
![]()
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Evident, o sa aplicam teorema lui Weierstrass.
a)
Ii faci monotonia: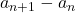 . Banuiesc ca o sa iasa
. Banuiesc ca o sa iasa
deci sirul este monoton crescator.
Acum marginirea.
Observam ca sirul nostru este pozitiv, pentru orice n natural. Deci putem spune ca . Acum trebuie sa ii gasim o margine superioara.
. Acum trebuie sa ii gasim o margine superioara.
Sunt mai multe metode prin care se poate face acest lucru. Cea mai evidenta este cea cu progresiile geometrice. Adica putem spune ca
iar suma din partea dreapta este o progresie geometrica usor calculabila. Pe aceeasi idee:
O luam pe a doua:
Calculam suma folosind formula sumei unei progresii geometrice:
Deci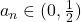
Sirul fiind monoton si marginit, conform teoremei lui Weierstrass, rezulta ca sirul este convergent.
Daca ar fi sa mergem după weierstrass atunci:
Mărginire :
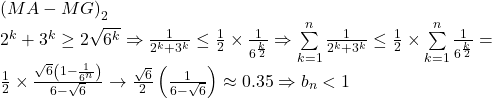
monotonie : este prea simpla ca s-o mai fac …. se studiază semnul b_(n+1)-b_n
Solutia 1)Cea mai puternica aproximare a bn pleacă de la inegalitatea mediilor:
Deci după cum vezi, bn tinde către 0.35 …. Eu am presupus imediat ca bn este mărginit superior de 1 (asa ca sa iasă frumos!)…
Solutia 2 si 3 sunt niste solutii foarte slabe dar mai simple … restrânge sirul bn direct la valoarea 1.
Pentru al doilea sir:
Monotonie:
Marginire:
Avem evident, .
.
Dar
(pur si simplu am amplificat fractiile)
de unde conchidem ca sirul este divergent.
Multumesc foarte mult! Am o nelamurire iarasi; Cum sa aflu marginirea sirului 1/(n+1) + 1/(n+2) + 1/(n+3) .. Din monotonia mi-a iesit ca e mai mic decat 0. Cealalta margina cum o aflu!
Monotonia o poti afla facand diferenta a doi termeni consecutivi (in cazul general) dar poti face si raportul a doi termeni consecutivi (numai atunci cand sirul are termeni pozitivi) si il compari cu 1. Asta ca idee.
Avem:
Deci sirul este strict crescator deoarece diferenta a doi termeni consecutivi este pozitiva.
La marginire:
Evident sirul este pozitiv, deci .
.
Dar
deci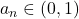 deci sirul este marginit. Fiind, de asemenea si monoton, rezulta ca sirul este convergent.
deci sirul este marginit. Fiind, de asemenea si monoton, rezulta ca sirul este convergent.