Va rog ajutatima in inteleg nimic din matematica :
|x| = 36 – cum se rezolva ?
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Modulul unui numar x poate fi egal cu insusi numarul,daca el este pozitiv sau cu opusul sau,daca el este negativ.Adica:
|x|=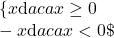
Deci in cazul tau,ecuatia |x|=36 are doua solutii:36 si -36
Modulul unui numar real ,.are rolul de a pune in evidenta numai „valoarea” numarului nu si semnul lui.Exemple;l5l=5 , l-9l=9 daca lxl=36 , x poate fi +36 sau -36. Se pote vedea ca (radical din x^2) este totdeauna pozitiv si se scrie ,corect, (radical din x^2)=lxl-modul de x. Functia „modul”se defineste , avand ca rationament cele de mai sus, astfel ;
f(x)=lxl=-x pentru x<o-(ex. x=-5 ->l-5l=-(-5)=5
…….lxl=0 pentru x=0
…….lxl=+x pentru x>0-ex. x=+4->l+4l=+(+4)=4
Functia „modul” este totdeauna pozitiva sau zero , dar niciodata negativa
Semnul modulului unei expresii matematice. Exlx-4l. Se ia x-4 si se egaleaza cu zero ->x-4=0are ca solutie pe x=4.Pentru orice valoare a lui x<4, x-4<0- adica este negativ. Pentru aceste valori ale lui x, lx-4l=-(x-4)=-x+4. pentru x=4, x-4=0 si lx-4l=0 , iar pentru x>4 , x-4 este pozitiv si
lx-4l=+(x-4)=x-4 Ajunge. Dumnezeu sa fie cu tine. Succes.