sa se rezolve:
1/{x} = 1/x + 1/[x]
o idee?
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Salut,
Îţi propun o soluţie, sper să îţi fie de folos.
Din enunţ observăm ceva important: membrul stâng este întotdeauna pozitiv, pentru că partea fracţionară {x} € [0, 1). Asta înseamnă că dacă vom avea vreo soluţie negativă, membrul drept va fi negativ, deci soluţia negativă nu este acceptată (1).
Altă observaţie, tot din enunţ]\{x\}\neq0[/tex],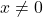 şi
şi ![Rendered by QuickLaTeX.com [x]\neq0](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-aeea82becee6b98511a6d98d6bd2fa31_l3.png) (2)
(2)
Strategia rezolvării acestui tip de probleme este exprimarea părţii fracţionare funcţie de partea întreagă.
Notăm pe [x] = k, unde k € Z*, număr întreg nenul şi notăm pe {x} = z, cu z € [0,1) (3).
Ştim bine că x = k + z (5). Deci ecuaţia devine:
Partea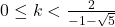 este absurdă pentru că un număr negativ nu poate fi mai mare decât zero. Deci avem:
este absurdă pentru că un număr negativ nu poate fi mai mare decât zero. Deci avem:
Dar k € Z* (mulţimea numerelor întregi, fără zero), deci k = 1. Înlocuim această valoare în expresia lui z, vezi relaţia 4 de mai sus:
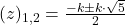 , adică
, adică 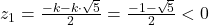 , nu este soluţie pentru că z € [0,1).
, nu este soluţie pentru că z € [0,1).
La final: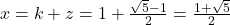 .
.
Deci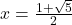 care este unica soluţie a ecuaţiei.
care este unica soluţie a ecuaţiei.
Green eyes.