Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Deci am de demonstrat:
a) Rad din n-rad din n-1< rad din n+1-rad din n, oricare ar fi n apartine N* (n> sau egal 1)
b) Rad din 2+rad 2+rad…+rad 2<2 (mentionez ca sunt radicali suprapusi,deci sirul de ceilalti radical e inclus in cel mare si tot asa, n nr de radicali)
Imi cer scuze ca am scris asa,sper sa se inteleaga,si sa ma pute-ti ajuta macar cu o sugestie, multumesc.
[/code]
Ma interesează problema b:
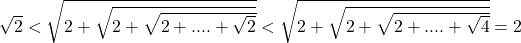
Multumesc foarte mult de ajutor, insa la punctul b nu prea am inteles.. ridic la patrat toti radicalii de sub radicalul mare?
Prin ridicare la patrat a expresiei din primul membru, va disparea primul radical . Radicalii din interiorul , primului radical , nu sunt afectati. Problema pe care ai dat-o a doua oara , se face ca si cea facuta de mine
Este o alternativa anevoioasa cu ridicatul la pătrat … uite te la indicatia lăsată de mine
Multumesc foarte mult de sfaturi, mi-au fost de ajutor la test😀 insa m-am mai gandit la punctul b, si am mai facut o metoda de rezolvare prin inductie.Oricum multumesc nespus! 😀 😀